Xiaotong – PhotoGeometry

A TUMAP issue

liuxiaotong2017July 25, 2019July 25, 2019Leave a comment

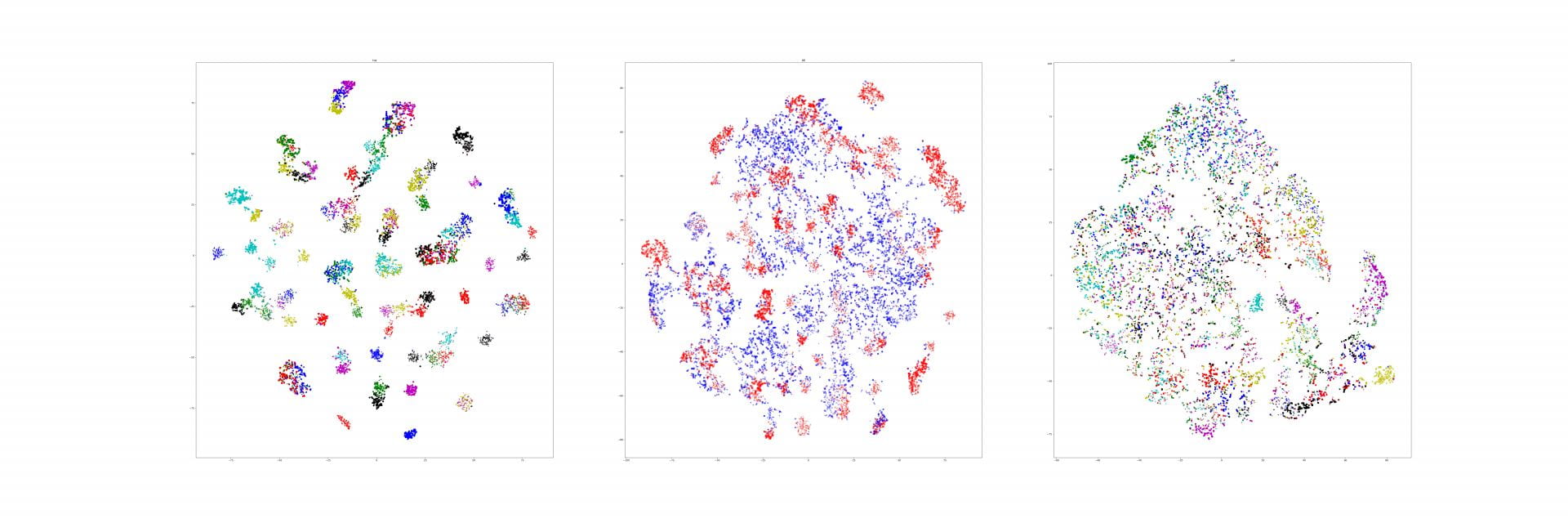
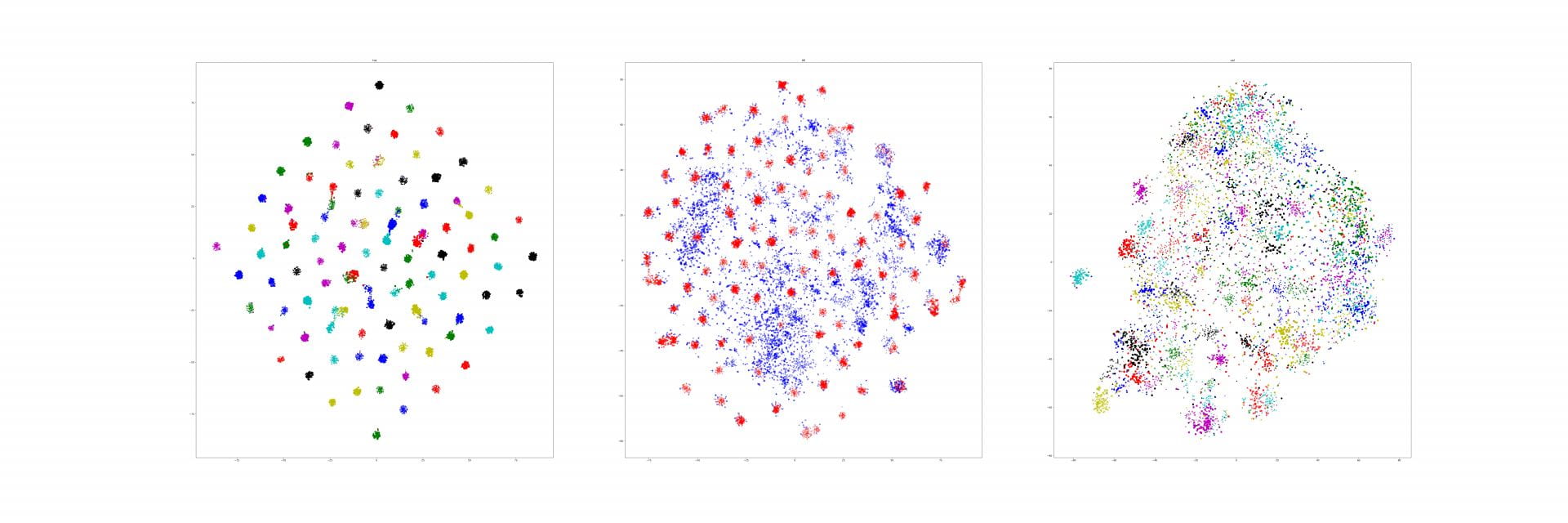
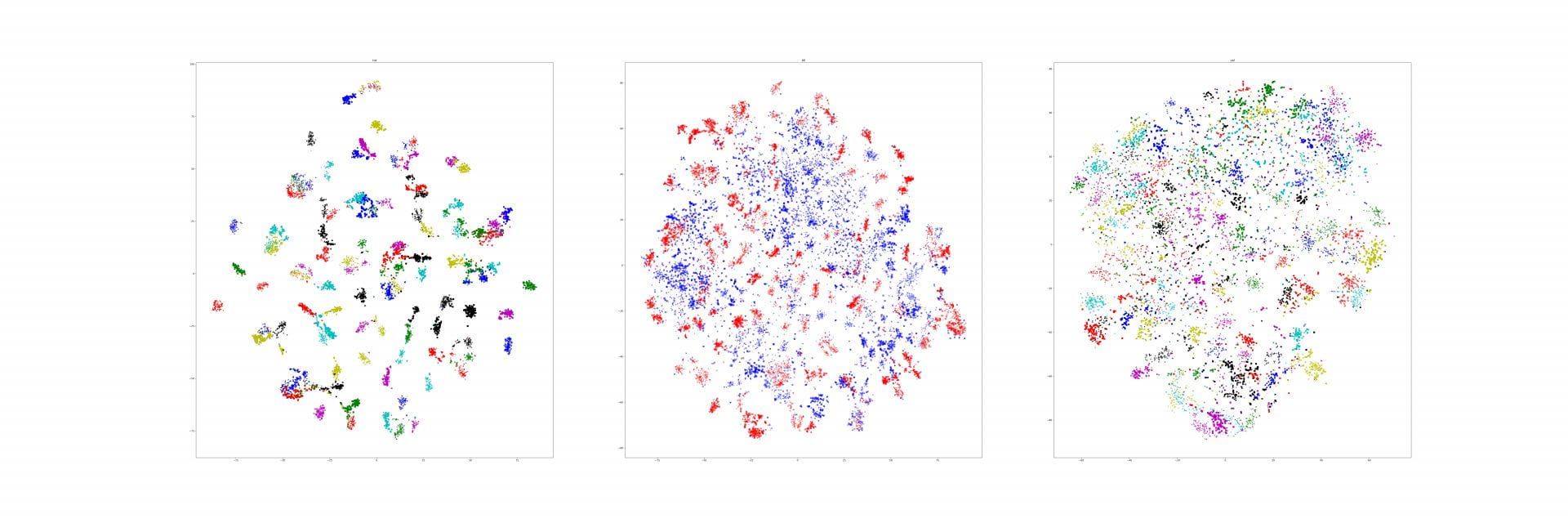
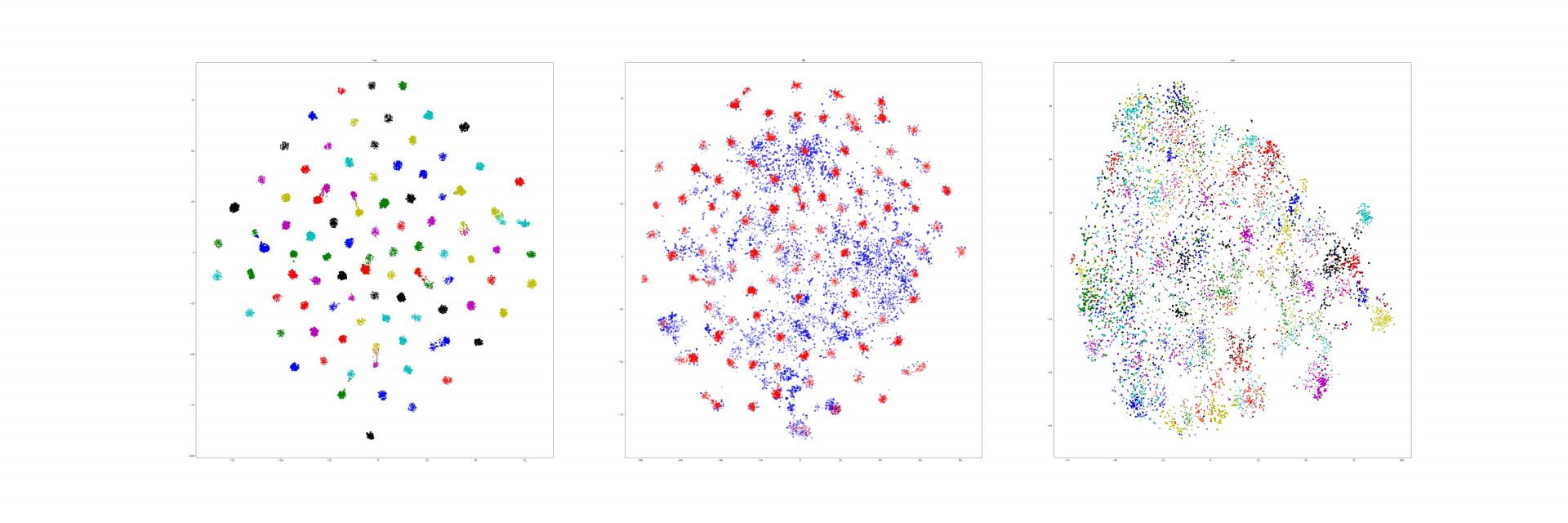
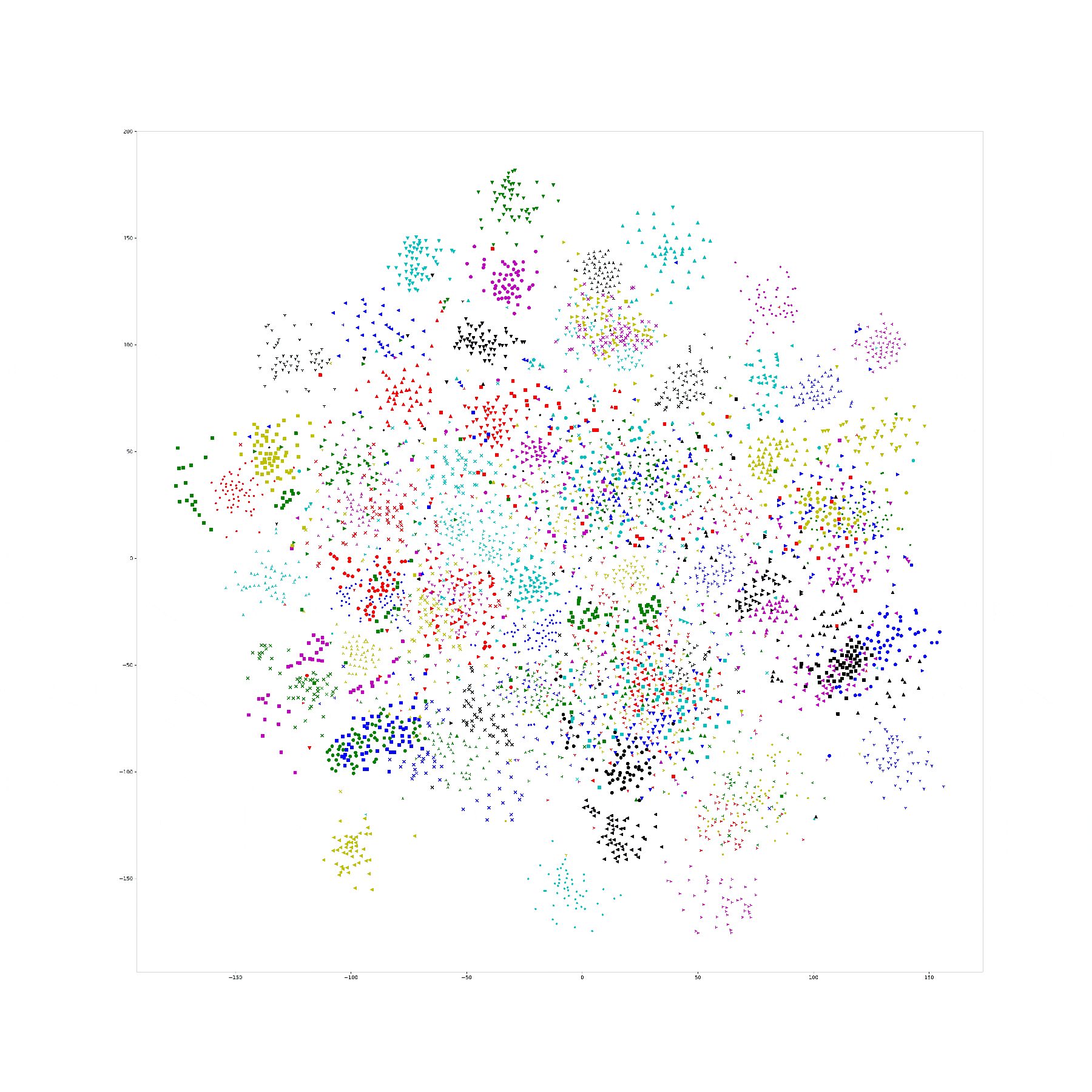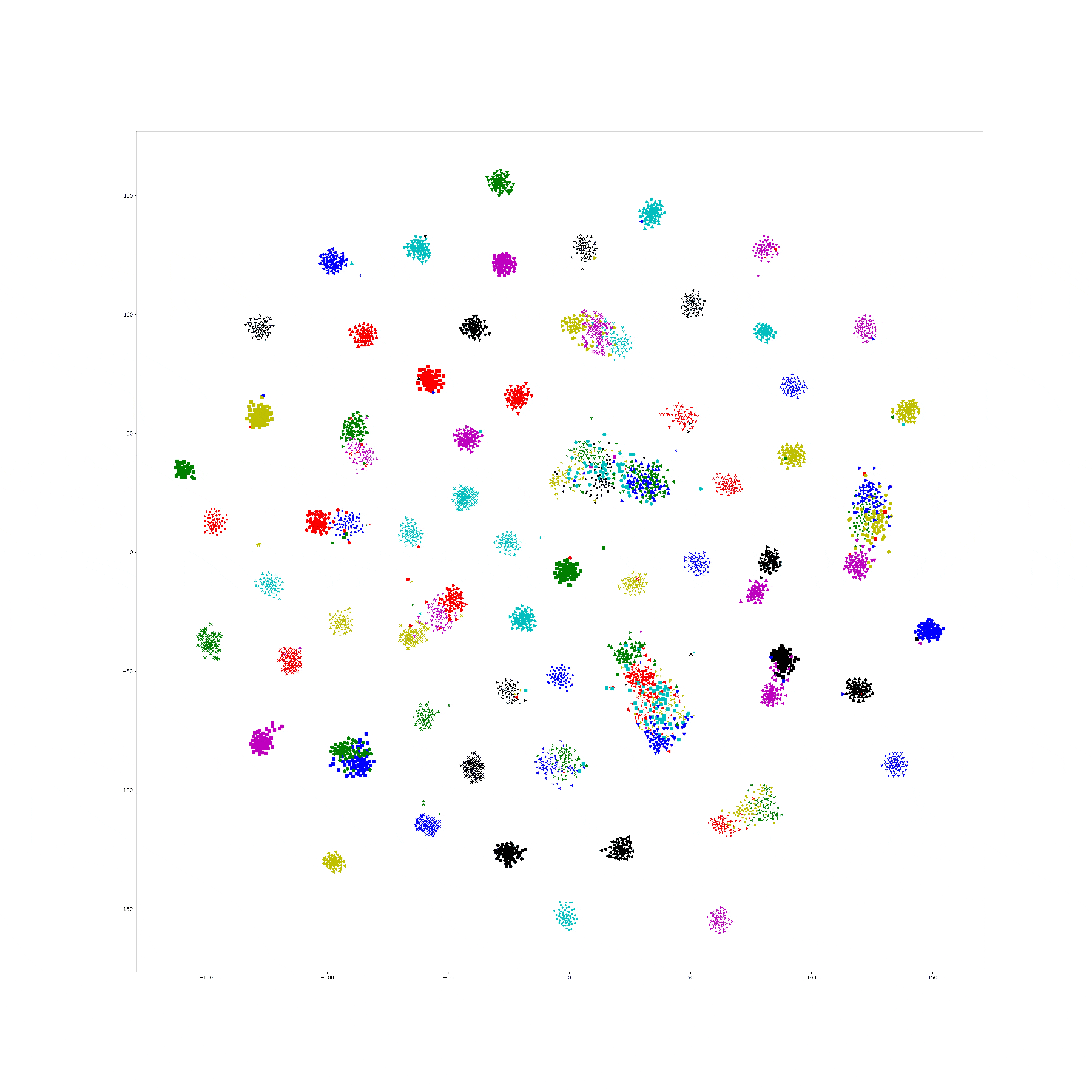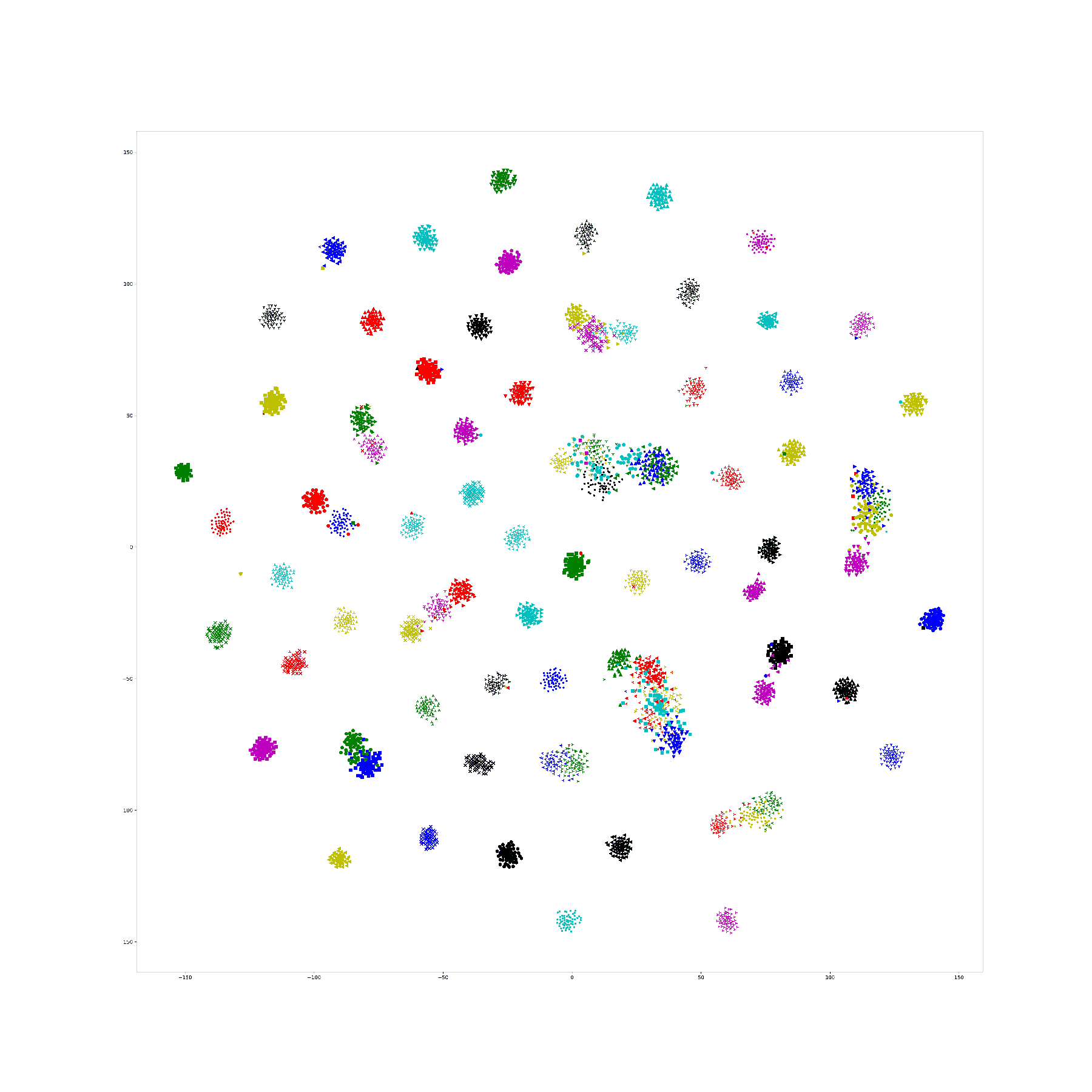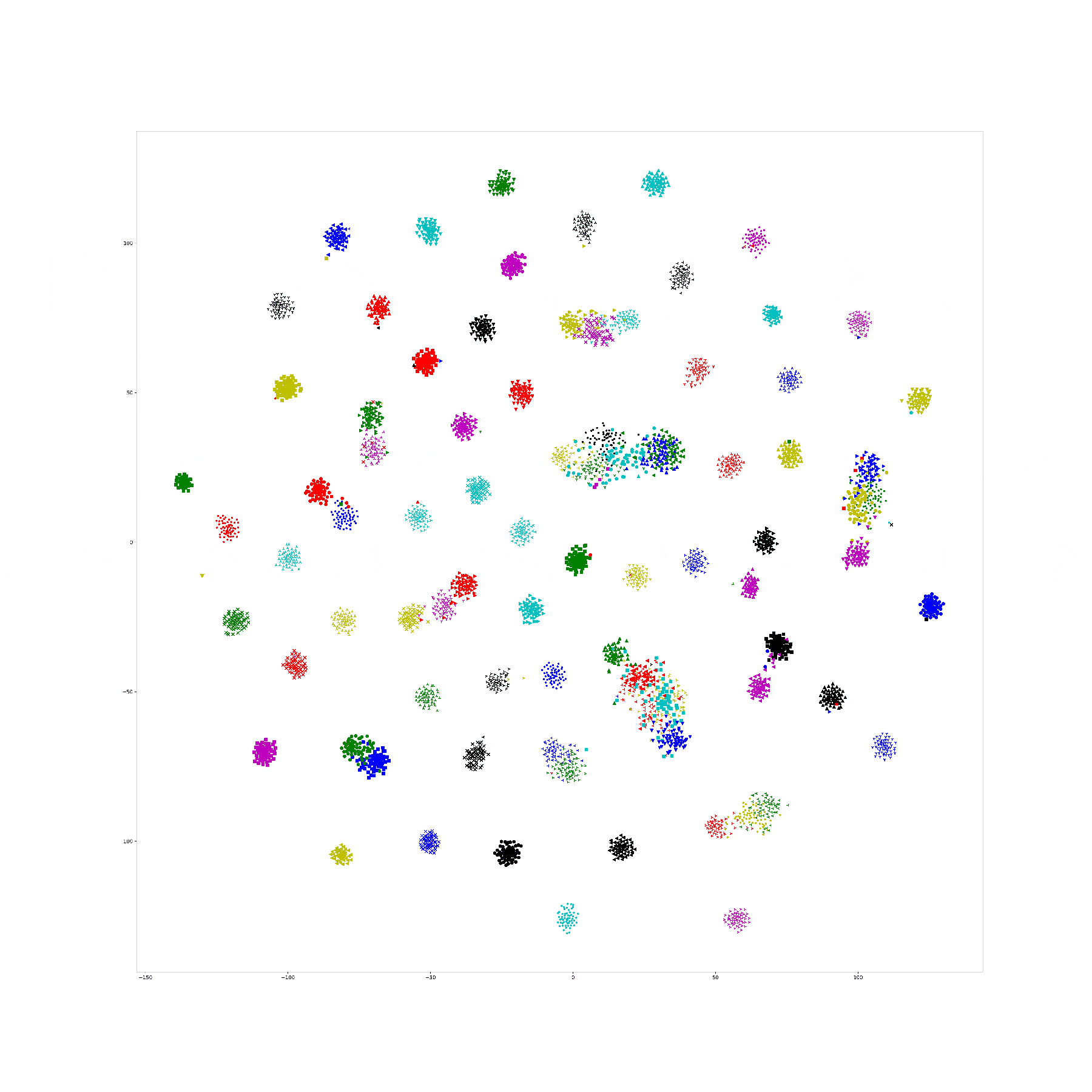
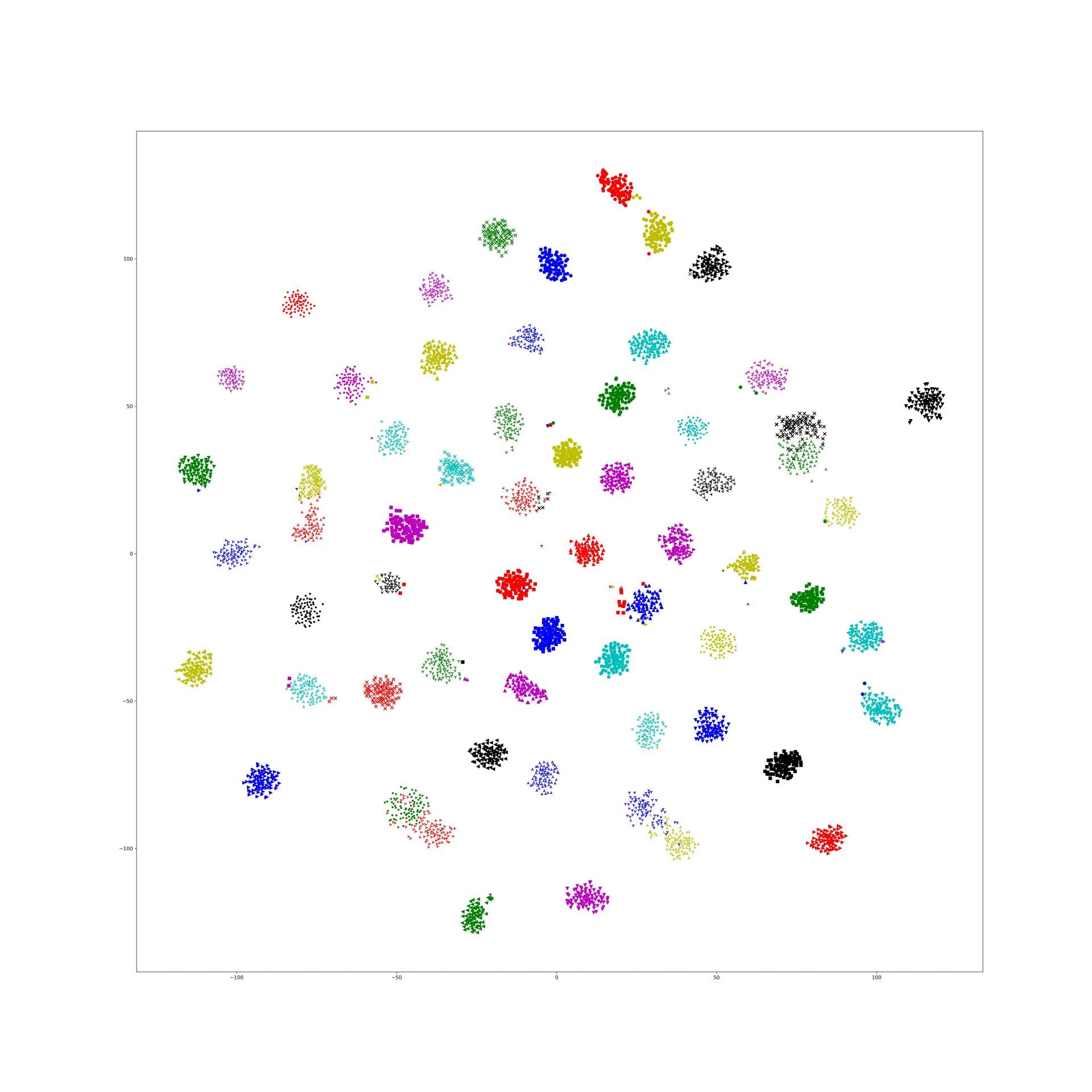
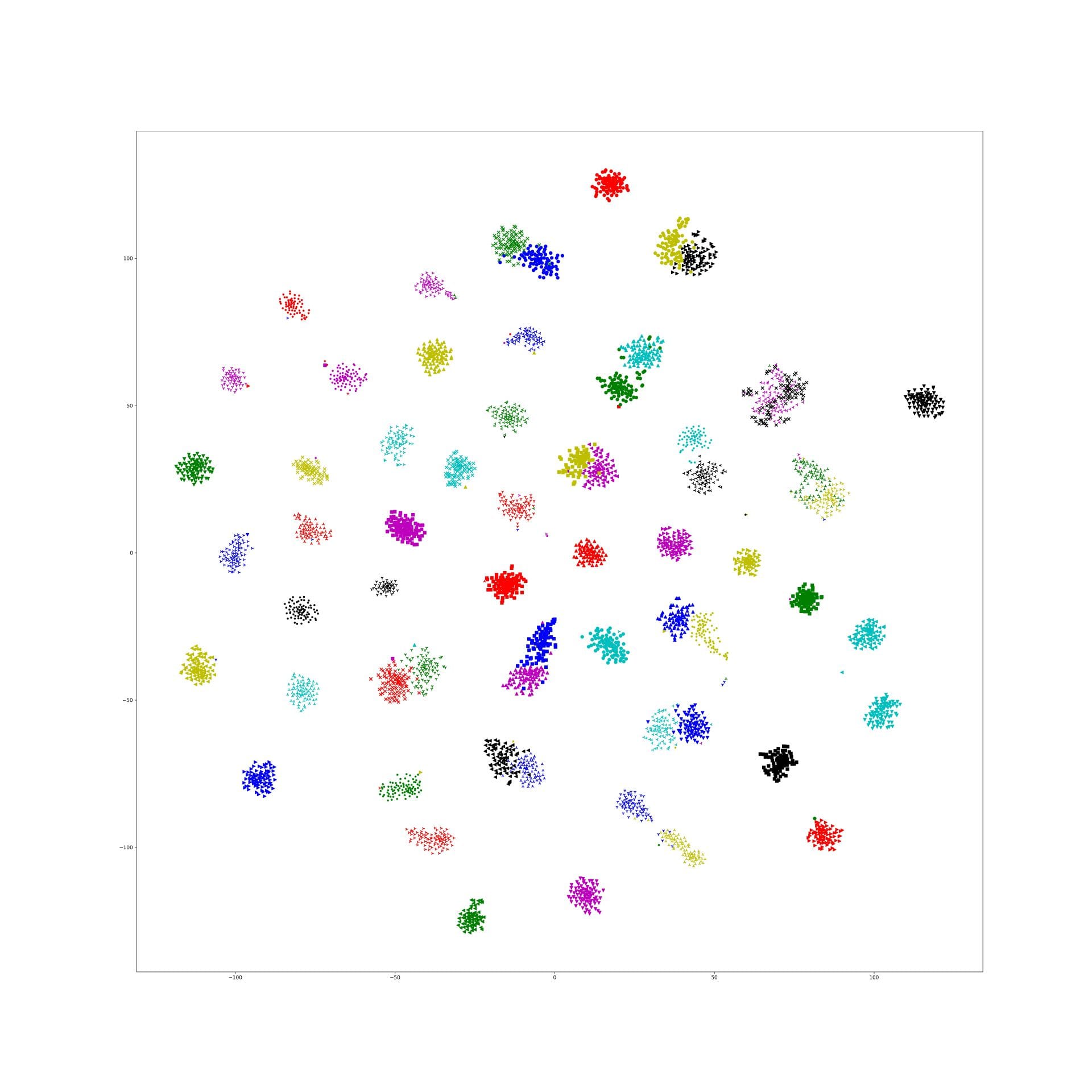
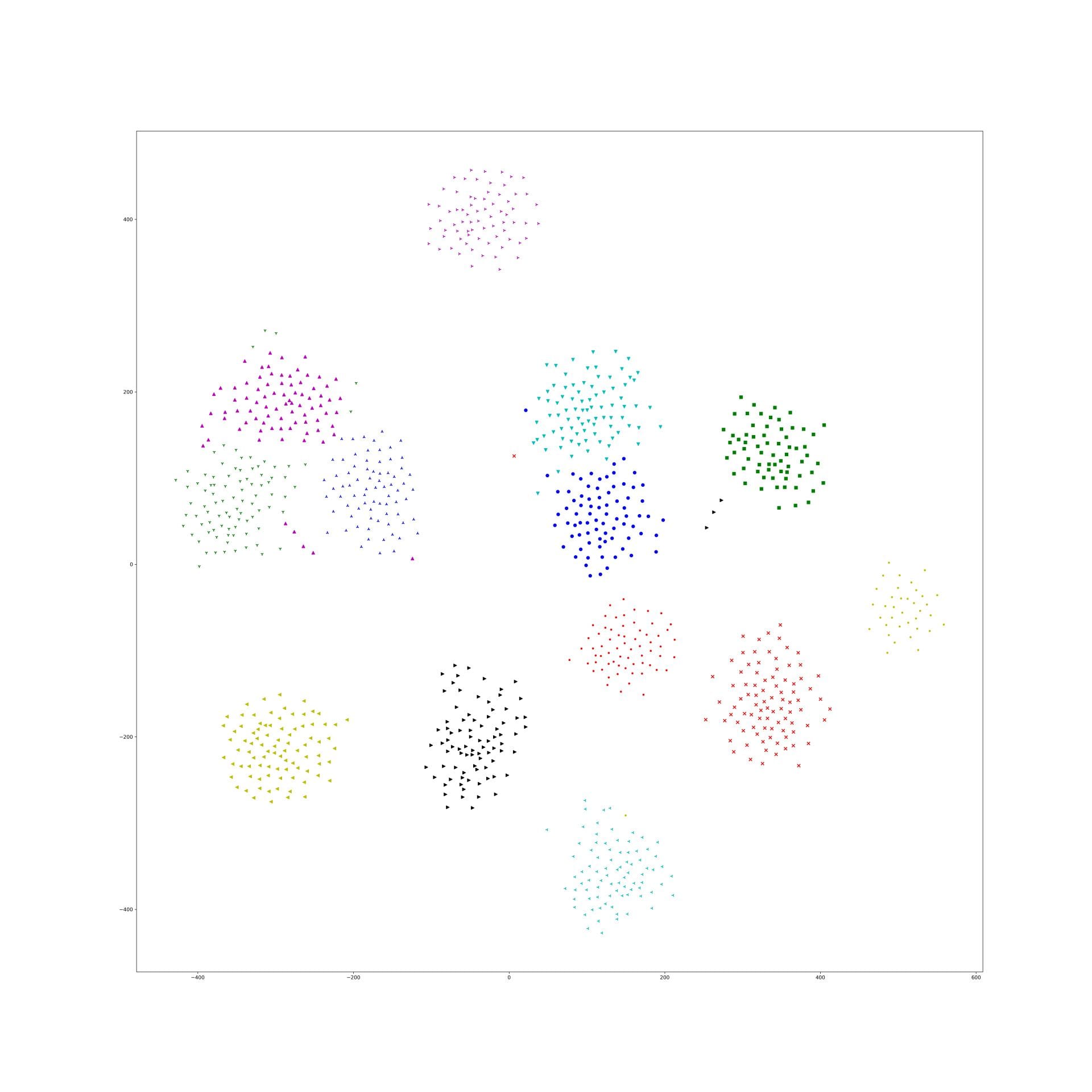
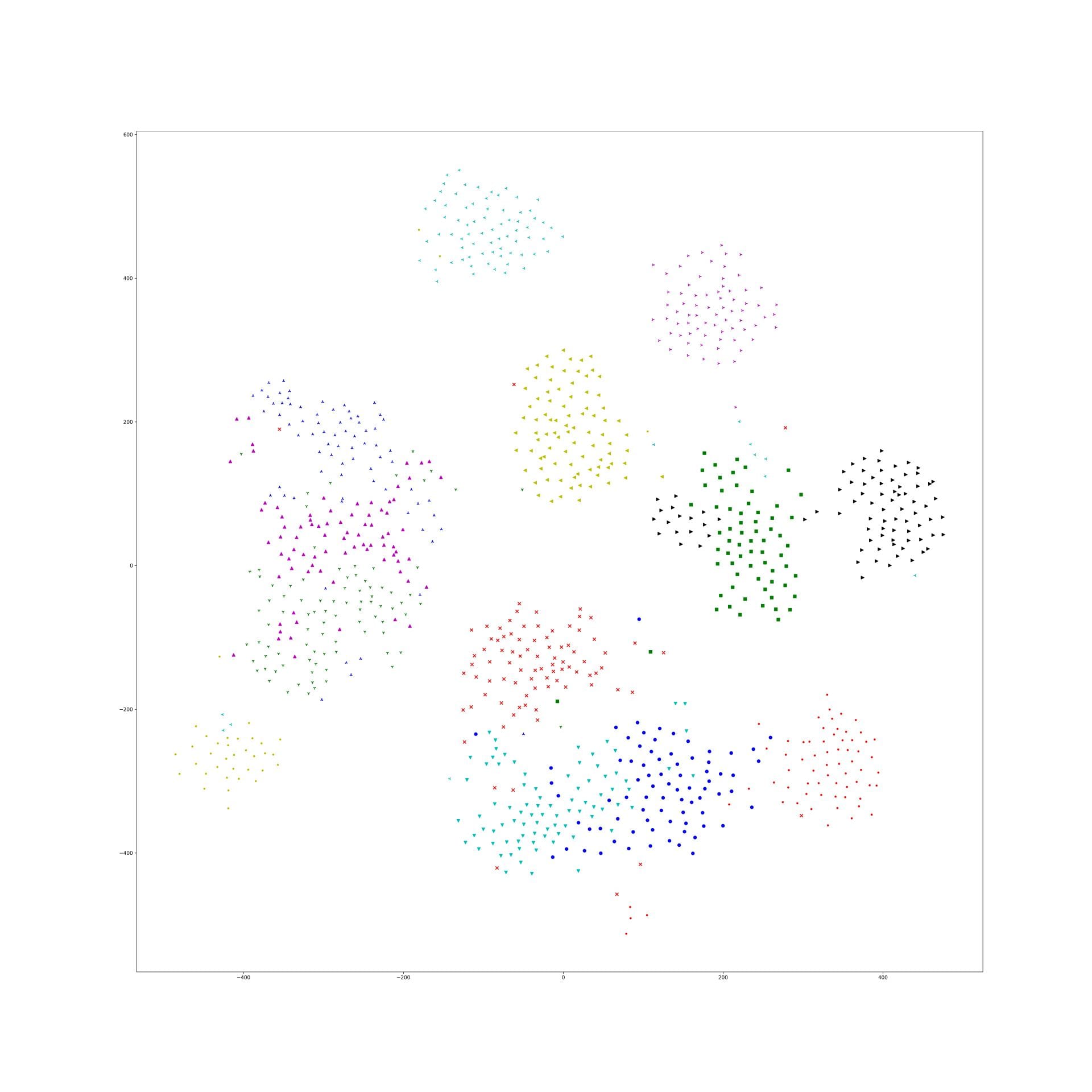
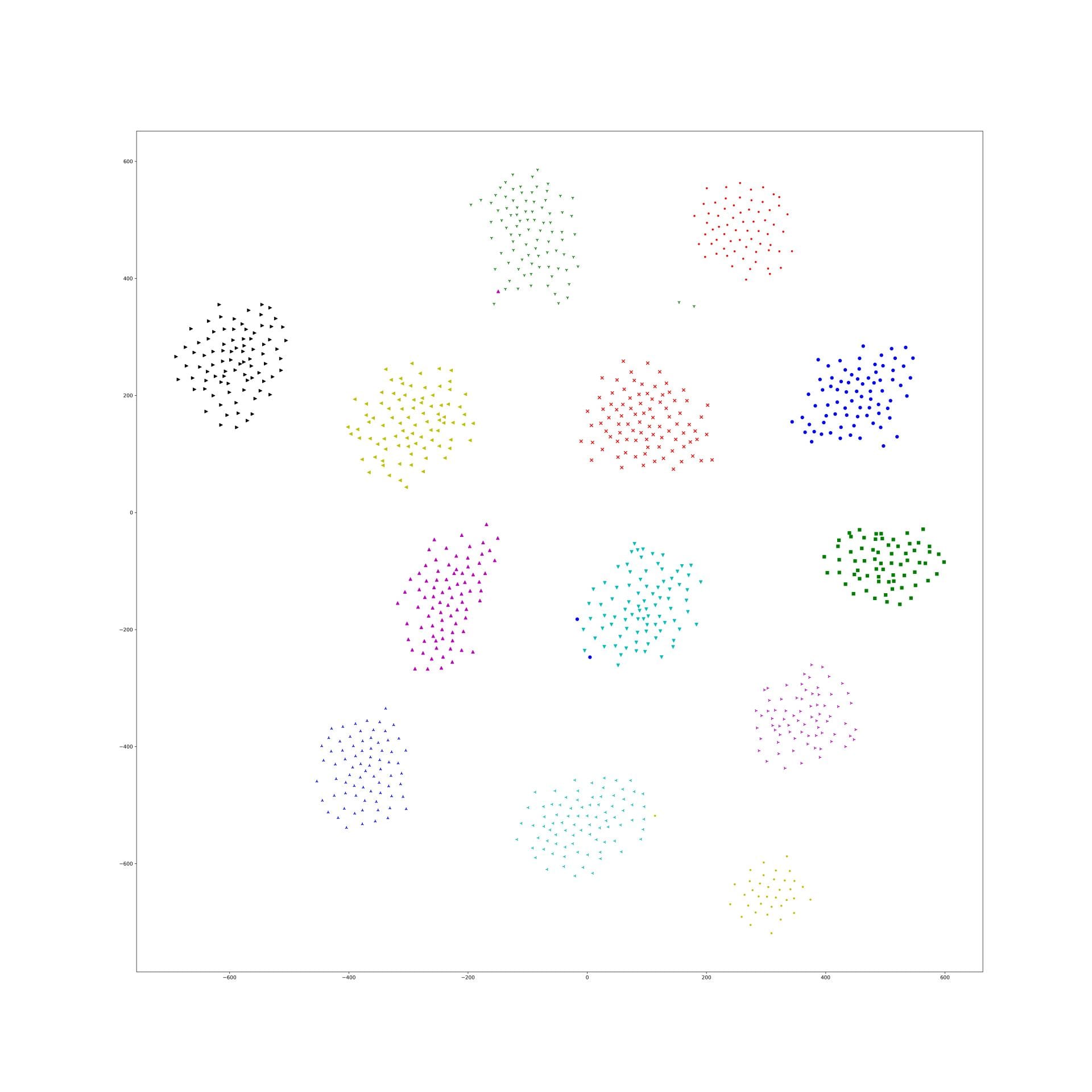
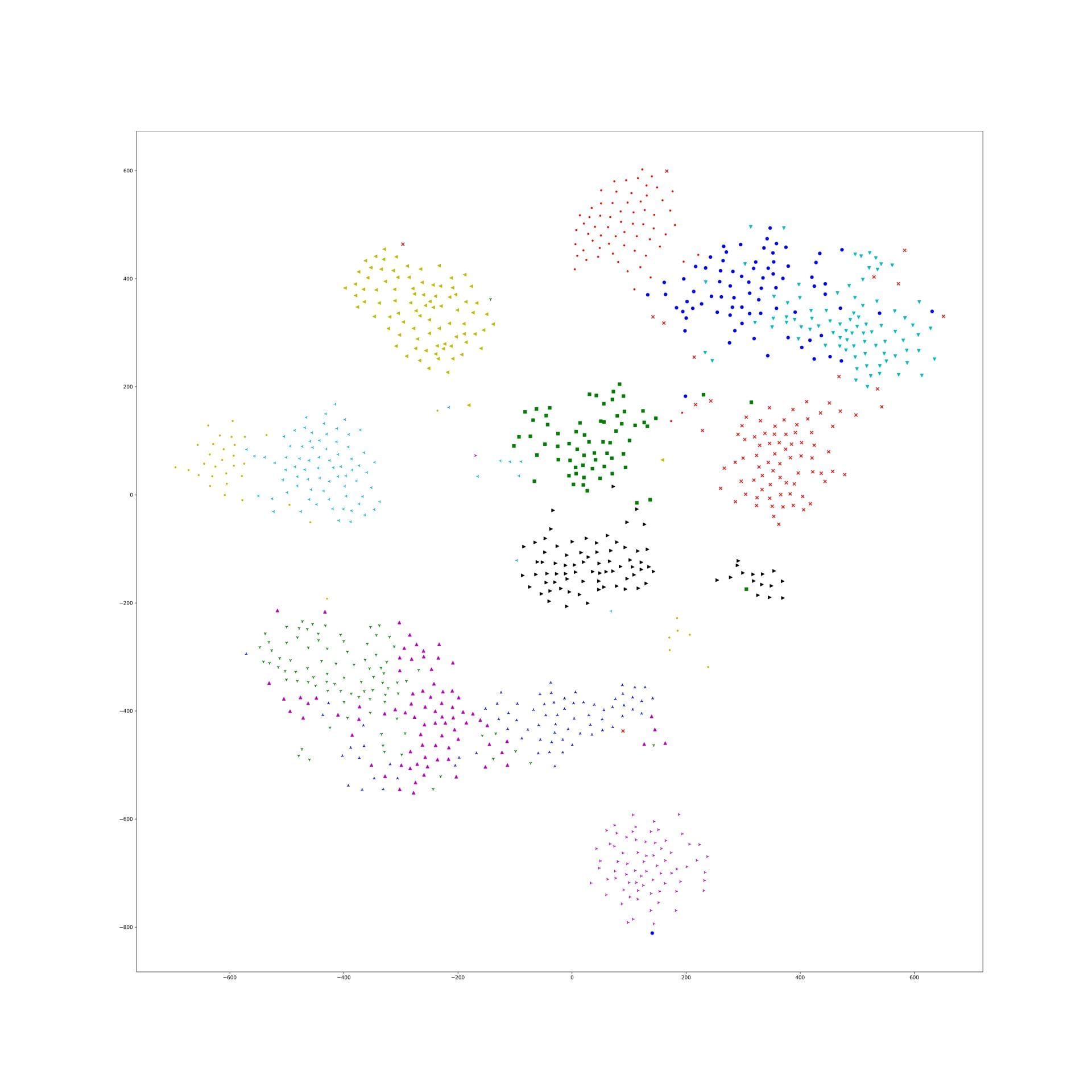
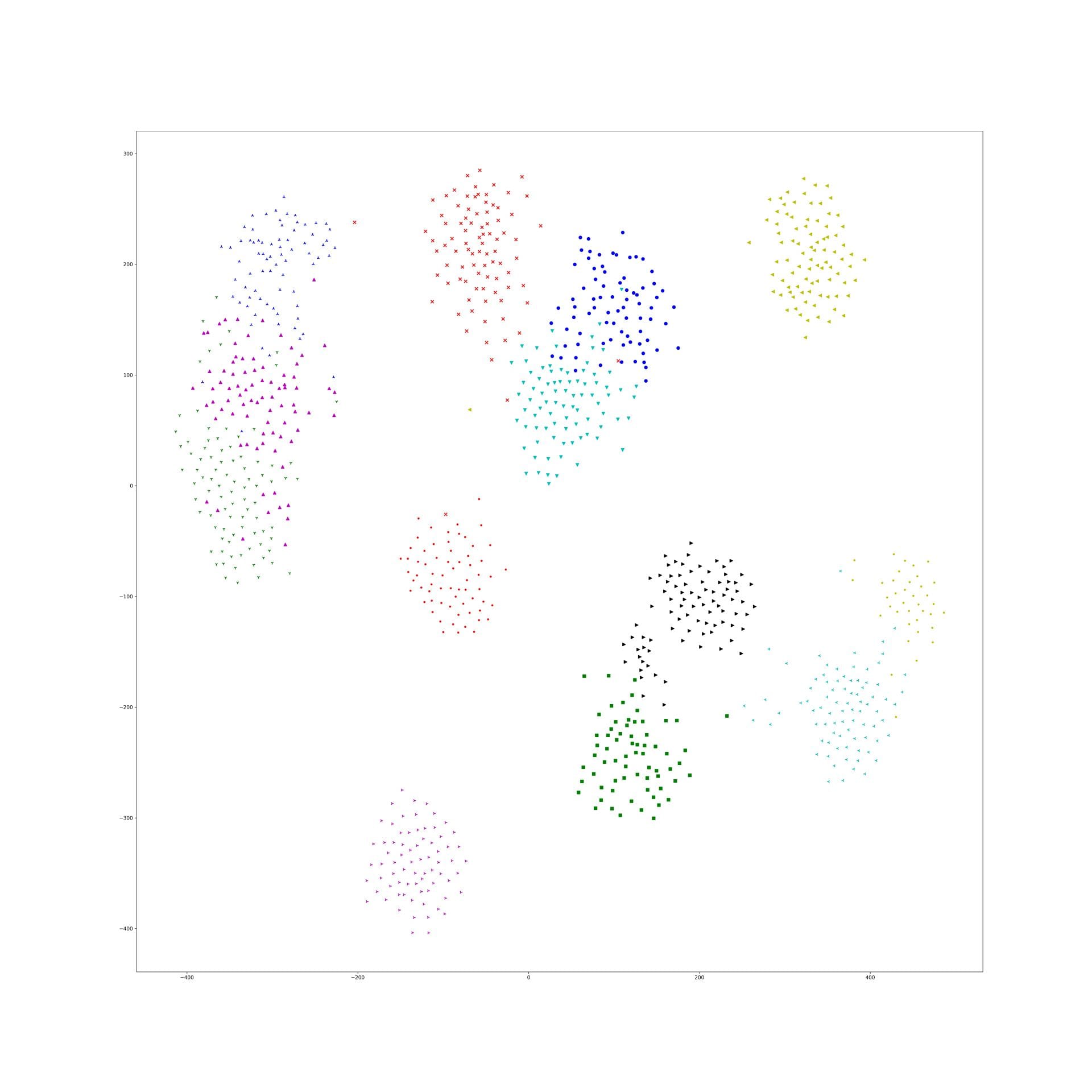
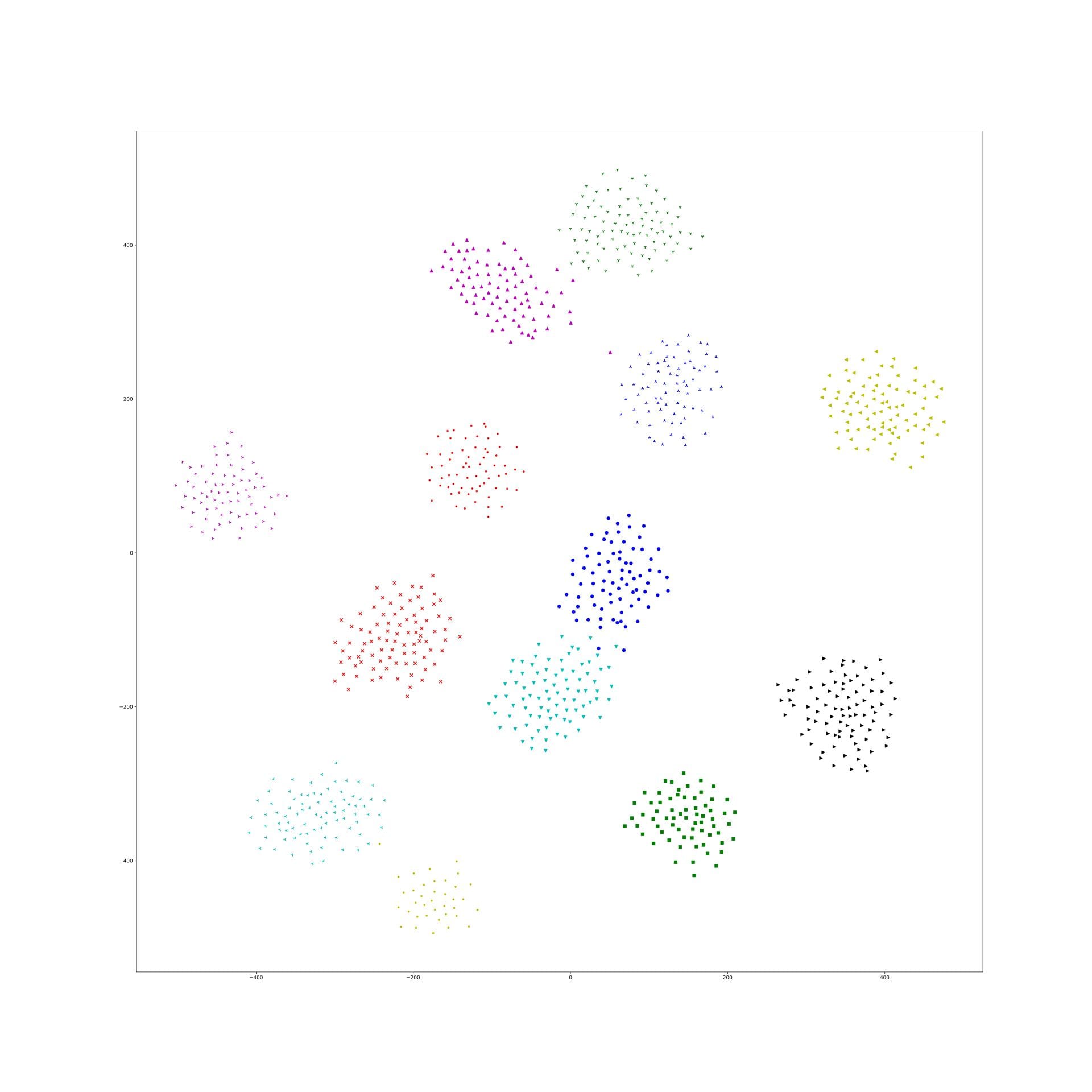
Last week, I find a problem of UMAP which is that if the high graph of a embedding representation is not connected, like NPair result on CAR training dataset, the optimizer of UMAP will keep push each cluster far away, which doesn't matter in visualization, but in TUMAP, we need to measure the loss of each map.

So, we try some different way to avoid or solve this problem.

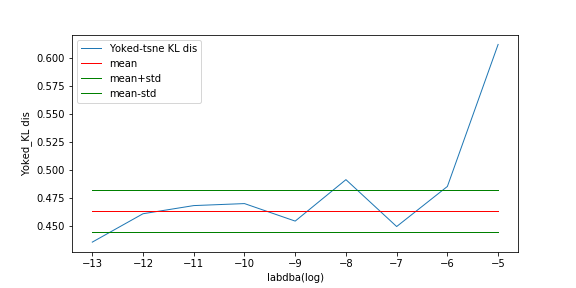
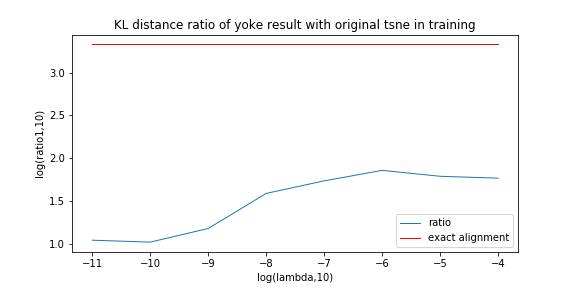
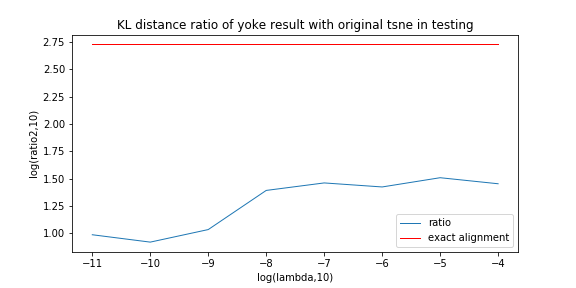
First, we compute KL distance of normal UMAP with TUMAP result instead of compare their loss.

Second, we try to optimize the repulsive gradient of edge in the high graph instead of each connection of every two points. But the result of this method gonna wired.

And, I try add a 0 vector into the high dimensional vectors, and make it equally very far from each points when constructing high-D graph. It doesn't work.

Some attempt on UMAP

liuxiaotong2017May 8, 2019May 8, 2019Leave a comment

UMAP paper: https://arxiv.org/abs/1802.03426

Here are some attempt based on a python module, umap-learn

First, we try UMAP on some Gaussian dataset.

(1): We generate two different Gaussian distribution dataset (1000*64,1000*64) in different location (mean), and visualize it by a)random pick two dimension b) umap, c) tsne.

(2): We generate two different Gaussian distribution dataset (1000*64,1000*64) in different scale (std), and visualize it by a)random pick two dimension b) umap, c) tsne.

(2): We generate two different Gaussian distribution dataset (1000*64,1000*64) in different location(mean) and scale (std), and visualize it by a)random pick two dimension b) umap, c) tsne.

Then, we try to compare result of t-SNE and UMAP on embedding result of npair and epshn, on CAR dataset.

Npair on training data:

Npair val data:

EPSHN tra data:

EPSHN val data:

t-sne plot for some Embedding methods on CAR dataset

liuxiaotong2017April 25, 2019April 25, 2019Leave a comment

In order to figure out generalization ability of different embedding method, I get feature vectors of CAR dataset which is training by different loss function.

For all loss function, the dataset is split into training data (first 100 categories) and validation data (rest). and it will show the t-sne for training, testing and all data following:

1. Lifted Structure (Batch All): training on Resnet-18.

2. Triplet loss (Semi-Hard Negative Mining): training on Resnet-18.

3.Easy Positive Semi-Hard Negative Mining: training on Resnet-18.

4. Npair Loss : training on Resnet-18:

5. Histogram loss: training on Resnet-50:

New test of yoke tsne on pytorch

liuxiaotong2017April 4, 2019Leave a comment

I calculate kl distances of same image pair by pytorch and sklearn code, and compare them. Unfortunately, they are different. So I check the pytorch code, find that the Q in pytorch have a little bug (add 2 instead of 1 in the numerator of Q). After fixing, they get same result now. I don't know how this bug will affect t-sne converge. So, I just re-run experiments. So far, experiments for all data in CUB dataset is done, for training data in CAR dataset is done.

The result is as following:

All of them are based on Npair loss

CAR_training dataset:

CUB_training dataset:

CUB_testing dataset:

And, I tried to visualize kl distance for each point in a tsne map.

Visualization about Npair loss training process by yoked t-sne

liuxiaotong2017February 21, 2019February 21, 2019Leave a comment

In last week we try to visualize the Npair loss training process by yoked t-sne. In this experiment, we use CUB dataset as our training dataset, and one hundred categories for training, rest of them for testing.

And, we train our Res-50 by Npair loss on those training data for 20 epoch, recording the embedding result for all training data in the end of each training epoch, and use yoked t-sne to align them.

This result is as following:

In order to ensure the yoked tsne didn't change the distribution too much, I record the KL distance of tsne plane with embedding plane for original tsne and yoked tsne. It seems that with training processing, the KL distance decrease on both original and yoked tsne. I think the reason is with limited perplexity, a structural distribution is easier to describe on tsne plane. And, the ratio between such KL distance between original and yoked tsne shows that the yoked tsne change a little bit in first three images (1.16, 1.09, 1.04) and keep same distribution in others (among 1.0).

Next step, drawing the image for each epoch is too coarse to see the training process, we will change to drawing image for each several iteration.

NEW IDEA: using yoked t-sne to find how batch size affect some embedding methods.

Comparing Npair loss with Proxy loss by yoke-tsne 1

liuxiaotong2017February 13, 20191 Comment

In last week, I do an experiment on comparing embedding result between Npair loss and Proxy-loss, for testing yoke-tsne.

Npair loss is a popular method which try to push point in different class away and pull point in same class close (like triplet loss) , while the proxy loss just assign a specific place for each category and just push all points in this category in this place. I expect to see this difference on embedding result by yoked tsne.

In this experiment, which is same to last two, CAR dataset is split into two part, and I just train our embedding on the first part (by Npair and Proxy loss) and visualize it.

This result is as following (left part is Npari loss and right part is Proxy loss):

Here is the original one:

Here is the yoked one:

The yoked figures shows some interesting thing about those two embedding method:

First, In Npair Loss result, there are always some points in different class in cluster while are not in Proxy Loss. Those points should be very similar to the cluster, and the reason why the Proxy loss doesn't have such points is that the proxy fixed all points in one class to same place, so those points was moved into their own cluster. Next step, I will find corresponding image for those points.

Second, they are more clusters mixed up in proxy loss, maybe its shows that proxy play a bed performance in embedding.

Third, the corresponding clusters is in some place and comparing to the original one, the local relationship doesn't change too much.

Some interesting embedding paper which visualized by t-sne

liuxiaotong2017February 11, 2019Leave a comment

Here is some interesting embedding paper which visualized by t-sne, if anyone know other paper, just write down in here.

[1]:Oh Song, Hyun, et al. "Deep metric learning via lifted structured feature embedding." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016.

[2]:Oh Song, Hyun, et al. "Deep metric learning via facility location." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2017.

[3]:Wang, Jian, et al. "Deep metric learning with angular loss." 2017 IEEE International Conference on Computer Vision (ICCV). IEEE, 2017.

[4]:Huang, Chen, Chen Change Loy, and Xiaoou Tang. "Local similarity-aware deep feature embedding." Advances in Neural Information Processing Systems. 2016.

[5]:Rippel, Oren, et al. "Metric learning with adaptive density discrimination." arXiv preprint arXiv:1511.05939 (2015).

[6]:Yang, Jufeng, et al. "Retrieving and classifying affective images via deep metric learning." Thirty-Second AAAI Conference on Artificial Intelligence. 2018.

[7]:Wang, Xi, et al. "Matching user photos to online products with robust deep features." Proceedings of the 2016 ACM on International Conference on Multimedia Retrieval. ACM, 2016.

More experiments about yoke-tsne on CAR dataset

liuxiaotong2017February 5, 2019February 5, 2019Leave a comment

Last experiment picked a particular lambda of yoke-tsne, and in this experiment, we pick up several lambda trying to see how lambda affect yoke-tsne.

As last experiment, we split Stanford Cars dataset in dataset A(random 98 categories) and dataset B(resting 98 categories). And, train Resnet-50 by N-pair loss on A, and get embedding points of those data in A. Second, train Resnet-50 by N-pair loss on dataset B, and using this trained model to find embedding points of data in dataset A. Finally, compare those two embedding effect by yoke-tsne.

In this measurement, with lambda change, we record the ratio between KL distance in yoke t-sne and KL distance in original t-sne, and record the L2 distance.

The result is as following:

We can see the KL distance ratio get an immediately increase when lambda is 1e-9. The yoke tsne result figure show that when lambda is 1e-8, the two result look like perfect aligned.

And, when lambda was downed to 1e-11, the yoke tsne seems no effect.

And, 1e-9 and 1e-10 works well, the training tsne get some local relation(between clusters) of testing one and keep the cluster inside relation:

Here is the original tsne:

Here is 1e-9:

Here is 1e-10:

In lambda 1e-9 1e-10, what is in our expectation, the location of each cluster is pretty same and the loose degree of each cluster was similar to the original t-sne.

For a reasonable lambda, I think it is depended on points number and KL distance between two embedding space.

An experiment of yoke-tsne on CAR dataset by N-Pair loss 3

liuxiaotong2017January 29, 20193 Comments

This experiment aims to measure whether a embedding method have a good generalization ability by yoke-tsne.

The basic idea of this experiment is trying to find the clustering effect of same category in training embedding and test embedding. In this experiment, we split Stanford Cars dataset in dataset A(random 98 categories) and dataset B(resting 98 categories). And, train Resnet-50 by N-pair loss on A, and get embedding points of those data in A. Second, train Resnet-50 by N-pair loss on dataset B, and using this trained model to find embedding points of data in dataset A. Finally, compare those two embedding effect by yoke-tsne.

The result is as following:

The left figure is the embedding result of dataset A as training data, and the right figure is the embedding result of dataset A as testing data. As we can see, the cluster in left figure is tight while the cluster in right part is looser. In spite of this, the points in left part was clustered into group, which means the generalization ability of N-Pair loss is not bad.

Next step, I want to try some embedding methods which are considered as bad 'generalization ability' to validate whether yoke-t-sne is a good tool to measure generalization ability.

Measurement for lambda selection to yoke tsne

liuxiaotong2017January 24, 2019January 24, 2019Leave a comment

In last week, we try our yoke t-sne method (add a L2 distance term into t-sne loss function). In this week, we try different scales of this L2 distance term to see the effect of t-sne.

This loss function of t-sne is that:

C = KL distance 1(embed 1 with t-sne1) + KL distance 2 + Ⲗ * (t-sne1 - t-sne2)^2

In this measurement, with lambda change, we record the ratio between KL distance in yoke t-sne and KL distance in original t-sne, and record the L2 distance.

The result is as following:

Its the ratio of for the first embedding.

Its the ratio of for the second embedding.

It this alignment error (the L2 distance)

As we can see in the above figures, we the weight of the L2 distance term increase, the ratio increase, which imply that when we 'yoke' heavier the t-sne, the distribution of t-sne plane is less like the distribution in high embedding plane. And, the decreasing alignment error shows that the two t-sne is align more perfect with lambda increasing.