Getting Ready for AAAI

Getting Ready for AAAI 2

AbbyJanuary 24, 20192 Comments

I was at the Danforth Plant Science Center all day yesterday as part of my on-boarding process. It was super fun -- lots of hearing stuff I didn't fully understand about plant biology, but also a lot of people excited to start thinking about imaging and image analysis in their work, plus the folks working on TERRA and TERRA adjacent stuff. Also gave a talk about vision for social good (finding a lost grave, using shadows to validate images on social media, TraffickCam) + visualization work. I was a bit worried it was light on anything having to do with plants at all, but folks seemed to love that. (A friend there specifically told me she was recruiting folks to attend by telling them it would be an hour without having to hear about plants.)

Today was spent putting together our poster for AAAI and working on getting the code finalized for release. The code repository is mostly ready to go but there's still a bit of work tomorrow to finish up on the re-producability section (re-producing our baseline results) and some of the evaluation code (all stuff that exists in the repo from the paper, just has to get cleaned up and moved over to the "published" repo).

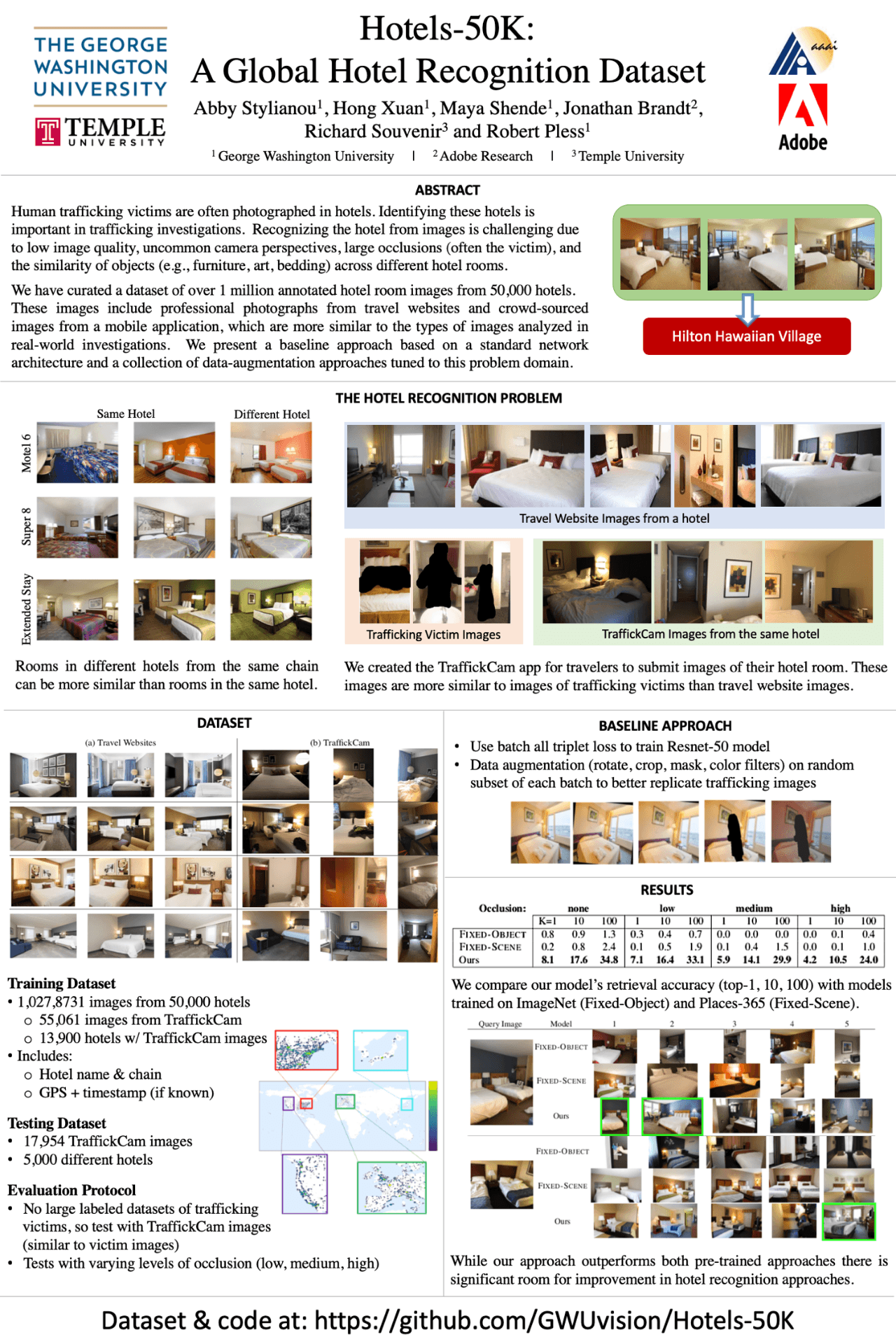
You can see our AAAI poster below. This is not my best poster by any stretch. It's a small format (28" x 42") and I kind of think I tried to fit too much on there. Part of me wanted to just put the title and a ton of pictures of hotels and tell the story at the poster. But my goals with posters are always to (1) make it coherent even if someone doesn't want to talk to me at the poster (I'm never a fan of posters that aren't clear without either reading the paper or having a 20 minute conversation with the author), (2) make sure there is a storyline that is clear and compelling and (3) not necessarily repeat every bit of information or experiment from the paper. I think this poster still meets those goals but does not do it as well or as cleanly as previous posters that I've made. We made some effort to remove extraneous bits and add some white space but it still feels super busy. Time constraints ended up driving me to just get it printed, as I'm heading out of town tomorrow night, but I kind of wish I'd started working on this early enough to have a few more cycles on it.

Yoke tsne by adding a L2 distance term in original loss function 3

liuxiaotong2017January 18, 2019January 24, 20193 Comments

As we known, t-sne focus on local relationship. In order to comparing two embedding result, we try to align those t-sne cluster into same place, which is intuitive to compare them.

The basic idea is adding a L2 distance term to align two t-sne embedding to together.

Here is the result:

Following is the original t-sne for two different embedding methods:

Following is the yoke t-sne for those two embedding result:

Using Simulated Glitter to Solve for Coefficients in Implicit Equation of Ellipse 1

mshendeJanuary 18, 20191 Comment

The implicit equation for an ellipse looks like f(x, y) = ax^2 + bxy + cy^2 + dx + ey + f = 0 . The idea here is that if we have at least five pieces of glitter that are "on" for some location of the camera and light (unknown), and we know the surface normals of those pieces of glitter, then we can use that information to determine the values of the coefficients in the implicit equation, thus defining a set of concentric ellipses associated with our set of "on" glitter. Then, we think the two foci of these concentric ellipses (which will be the same for each ellipse in the set) will define the camera and light locations.

10 pieces of glitter are "on", and the light and camera lie alone a vertical line.

In this image, we can see a sample simulation in which there are 10 pieces of glitter, all of which are "on", and the camera and light are location along a vertical line. Here, we expect to see a set of concentric, vertically oriented (major axis aligned with the y-axis) ellipses such that each ellipse is tangent to at least one piece of glitter.

Previously, we thought that this set of concentric ellipses may be defined by some a, b, c, d, and e that are fixed for the whole set of ellipses, and an f which is different for each of the ellipses. In other words, a, b, c, d, and e defined the shape, orientation and location of the ellipses and f defined the "size" of each ellipse.

I am starting to believe that this is not quite true, and that the "division of labor" of the coefficients is not so clearly defined. Perhaps it is the case that there is some function which defines how the coefficients are related to each other for a given set of concentric ellipses, but I am not sure what that function or relationship is.

Test Blog Post Jan 18

dtlafeverJanuary 18, 2019Leave a comment

This is a test post for the blog!

Photogeometry Research Group 1

plessApril 21, 2017March 21, 20181 Comment

Welcome to our lab blog!

We build cameras, algorithms, and systems that analyze images to understand our world in new ways. This page helps keep our lab organized:

Upcoming Conferences

Lab Members

Science and engineering thrives on diverse perspectives and approaches. Everyone is welcome in our lab, regardless of race, nationality, religion, gender, sexual orientation, age, or disabilities. Scientists from underrepresented groups are especially encouraged to join us.