Roughly the first four weeks of the project were spent characterizing a glitter sheet (estimating the position and orientation of thousands of glitter specs). All that work was done as a necessary first step towards the ultimate goal of calibrating a camera using a single image of a sparkly sheet of glitter. Camera calibration is the task of estimating the parameters of a camera, both intrinsic - like focal length, skew, and distortion - and extrinsic - translation and rotation. In glitter summer week 5, we tackled this problem, armed with our hard-earned characterization from the first four weeks.
We break the problem of camera calibration into discrete steps. First, we estimate the translation. In our camera calibration image we find the sparkling specs. A homography (found using the fiducial markers we have in the corners of the glitter sheet) allows us to map the coordinates of the specs in the image to the canonical glitter coordinate system, the system in which our characterization is stored. Sometimes the specs we map into the glitter coordinate system are nearby several characterized specs, and it is not clear which one of those specs we are seeing sparkle. So, we employ the RANSAC algorithm to zero in on the right set of specs that fit the model. We trace rays from the known light position, to the various specs, and then back into the world. Ultimately we find a some number of specs whose reflected rays all go very near each other in the world, and we use this "inlier" set to estimate the camera position.
Here is an image showing the rays reflected back from the glitter, zoomed in to show how many of them intersect within a small region. There are also outliers. The inliers are used to make a camera position estimate by searching over many positions and minimizing an error function that sums the distances from the position to the inlier rays. The estimated position is shown as well as the position we measured with traditional checkerboard calibration.
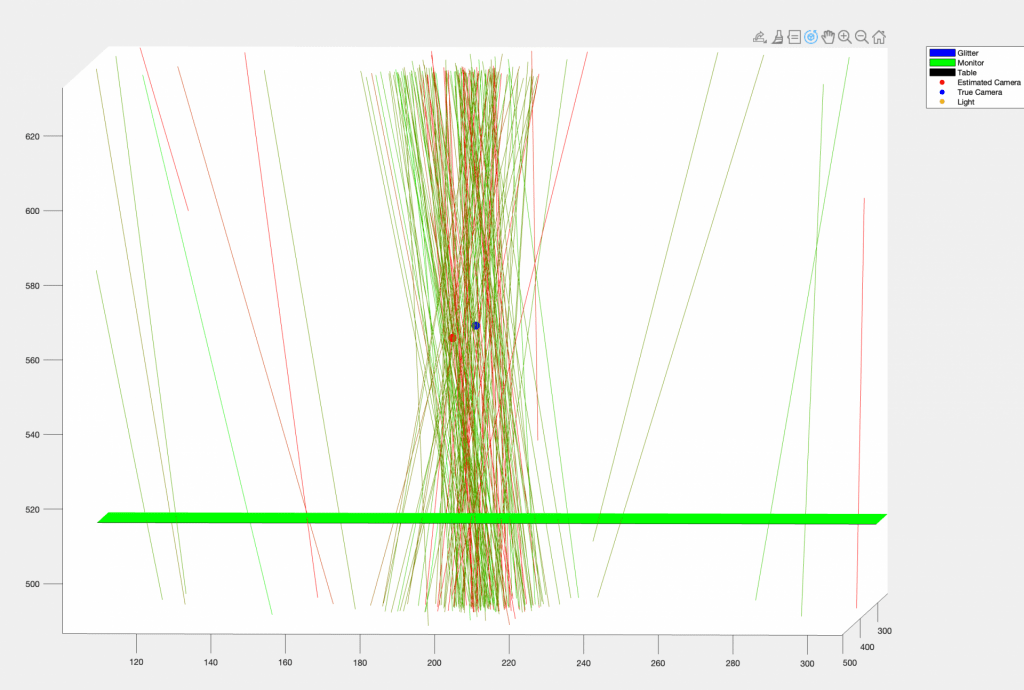
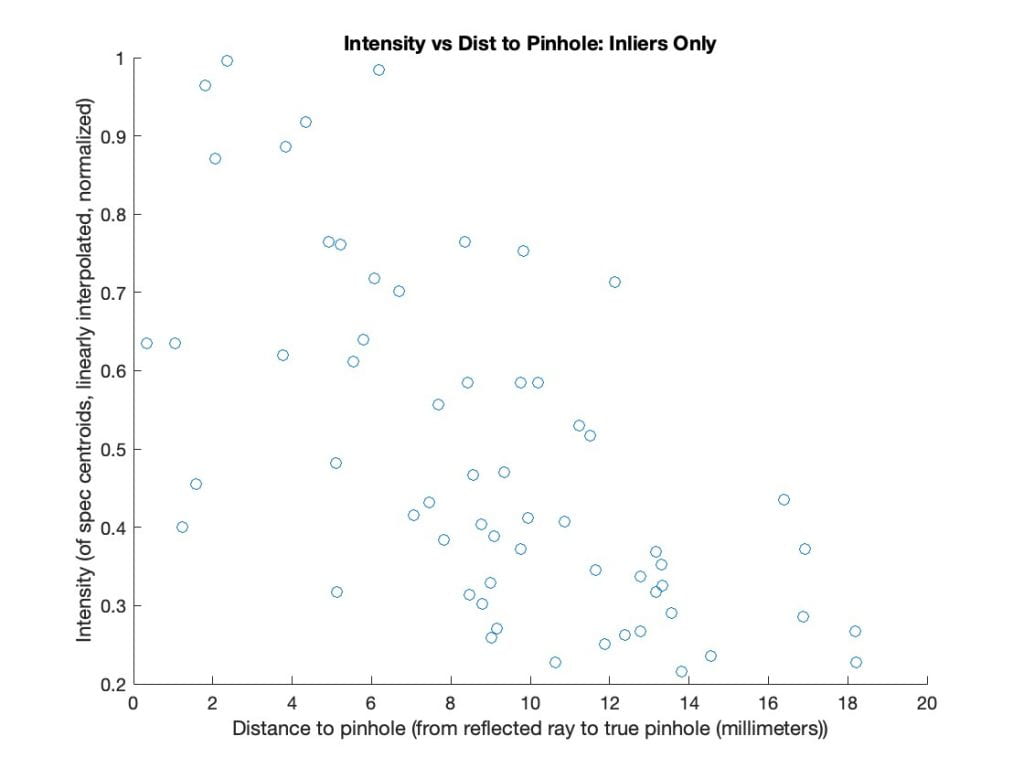
The camera position estimate is about 1 centimeter off. Not bad, but not the accuracy we are hoping for in the end. One way to improve accuracy could be to use the brightness of specs in the error function. Brighter specs should give tighter constraints on the position. Here is a plot showing the brightness of specs as a function of how closely their reflected rays pass by the camera position.
Next up is the rotation of the camera (where it is pointed in space) and the intrinsics. We begin with just a subset of the intrinsics we could ultimately estimate: focal length (in x and y directions) and skew. This is a total of 6 parameters we are estimating (3 for rotation and 3 for intrinsics). Since we know some points in the scene (fiducial markers and glitter specs in the characterization), we can find correspondences between points in the image and points in the world. For a point p in the image and corresponding point P in the world, our estimate of the rotation matrix R, intrinsics matrix K, and (already found) translation matrix T should give us p ~ KR(P-T). Our code seems to have worked out well. Here is a diagram showing the observed image points in green and where our estimates of translation, rotation, and intrinsics matrix project the known world points onto the image.
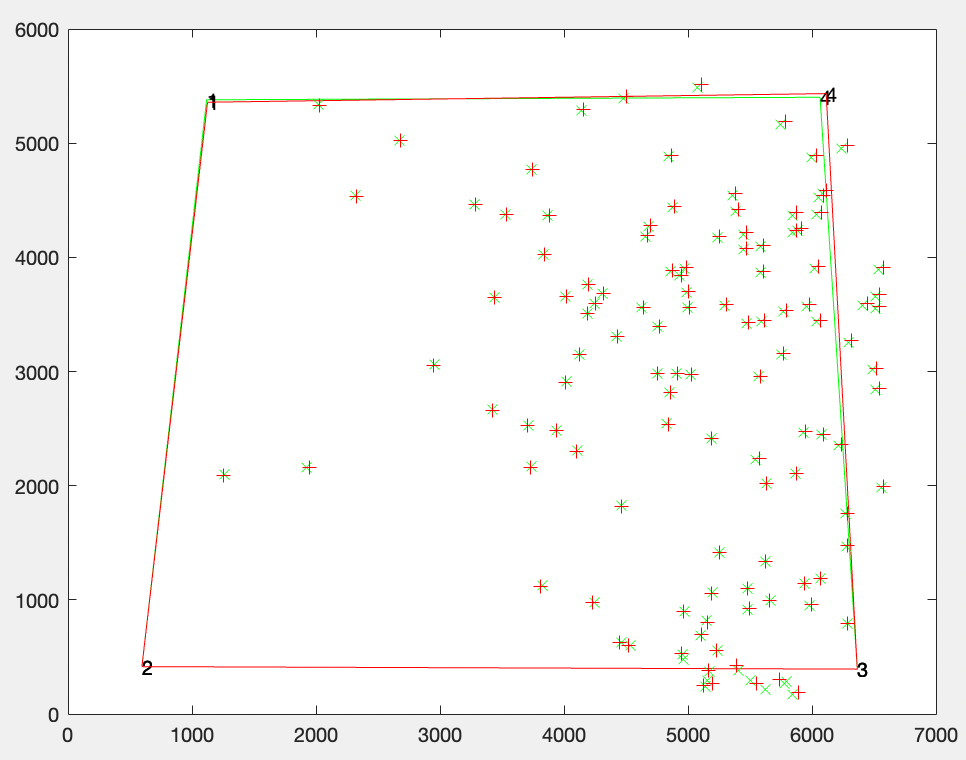
This is very exciting! As week five comes to a close, we have code to (a) characterize a sheet of a glitter and (b) calibrate a camera with a single sheet of glitter. Next week we will look to analyze our calibration by comparing the results to traditional (checkerboard) calibration techniques. Thereafter, we will be looking to reduce error (improve accuracy) and estimate additional intrinsic parameters like distortion! We have some fun ideas for how to improve our system, and we are excited to press forward.