5 | INTRODUCTION TO DIFFERENTIATION
5 | INTRODUCTION TO DIFFERENTIATION
This chapter of Single Variable Calculus by Dr JH Klopper is licensed under an Attribution-NonCommercial-NoDerivatives 4.0 International Licence available at http://creativecommons.org/licenses/by-nc-nd/4.0/?ref=chooser-v1 .
5.1 Introduction
5.1 Introduction
There are two main sections in the study of calculus. These are differentiation and integration. In this chapter we start the study of differentiation.
5.2 Slope
5.2 Slope
A curve on the Cartesian plane can be the visual representation of a function in a single variable . For every value , the function calculates an output . Where is a value on the horizontal real number line, we have that is a value on the vertical real number line.
f
x
x
y=f(x)
x
y
We can calculate a slope of a line that connects any two points on the curve of the function.
f(x)=+5,x∈[0,5]
2
x
(
1
)We can consider the two points and , where we calculate =f() and =f() in (2).
(,)=(,f())=(2,f(2))=(2,9)
x
1
y
1
x
1
x
1
(,)=(,f())=(4,f(4))=(4,21)
x
2
y
2
x
2
x
2
y
2
x
2
y
1
x
1
f(2)=+5=9f(4)=+5=21(,)=(2,9)(,)=(4,21)
2
2
2
4
x
1
y
1
x
2
y
2
(
2
)Definition 5.2.1 The slope, , of a line between two points, and , on the curve of a single variable function is the ratio of the difference between and to the difference between and , shown in (), where is the difference in and is the difference in .
m
(,)
x
1
y
1
(,)
x
2
y
2
y
2
y
1
x
2
x
1
Δy
y
Δx
x
m=--=-m==
y
2
y
1
x
2
x
1
f()-f()
x
2
x
1
x
2
x
1
Δy
Δx
rise
run
(
3
)Note that we commonly refer to the rise-over-run definition.
Problem 5.2.1 Calculate the slope of a line in the Cartesian plane between the points and .
(2,1)
(5,3)
To solve this problem we assign the points as and . We use (3) to calculate the slope using code.
(,)=(2,1)
x
1
y
1
(,)=(5,3)
x
2
y
2
In[]:=
3-1
5-2
Out[]=
2
3
The slope of the line in the Cartesian plane between the two points is . For a change in the value of , we see a rise in the value of . Figure 5.2.1 shows the two points in the Cartesian plane and the line segment between them.
2
3
x
1
y
2
3
In[]:=
Show[ListPlot[{{2,1},{5,3}},PlotRange->{{0,6},{0,4}},PlotLabel->"Figure 5.2.1",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large],Graphics[{Orange,Line[{{2,1},{5,3}}]}]]
Out[]=

In the case of two points in the Cartesian plane with the same value, we have a vertical line segment. Using () we have a denominator that is , which mean the slope is undefined. In the case that two points in the Cartesian plane has the same values (but different values), then the denominator of () is and the slope is . While the slope in Problem 5.2.1 was positive, we can also have a negative slope.
x
0
y
x
0
0
Problem 5.2.2 Calculate the slope of a line in the Cartesian plane between the points and .
To solve this problem we assign the points as and . We use (3) to calculate the slope using code.
(1,3)
(4,1)
To solve this problem we assign the points as
(,)=(1,3)
x
1
y
1
(,)=(4,1)
x
2
y
2
In[]:=
1-3
4-1
Out[]=
-
2
3
The slope of the line in the Cartesian plane between the two points is . For a change in the value of , we see a fall in the value of . Figure 5.2.2 shows the two points in the Cartesian plane and the line segment between them.
-
2
3
x
1
y
2
3
In[]:=
Show[ListPlot[{{1,3},{4,1}},PlotRange->{{0,5},{0,4}},PlotLabel->"Figure 5.2.2",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large],Graphics[{Orange,Line[{{1,3},{4,1}}]}]]
Out[]=

Given the slope of the line between the two points, we can calculate a function that has a graph that passes through the two points on the curve.
Definition 5.2.1 The secant line to a curve of a single variable function is the graph of a line that passes through two arbitrary points of the curve , shown in ().
f
f
y-=m(x-)y-f()=mx-y=-x--+f()
y
1
x
1
x
1
mx
1
f()-f()
x
2
x
1
x
2
x
1
f()-f()
x
2
x
1
x
2
x
1
x
1
x
1
(
4
)Figure 5.2.3 shows the curve (blue) of the function in (1), together with the two points on the curve and and the secant line (orange) of the function, , calculated from (4) and shown in (5).
(,)=(2,9)
x
1
y
1
(,)=(4,21)
x
2
y
2
g
g(x)=x-(2)+9g(x)=x-(2)+9g(x)=6x-12+9g(x)=6x-3
21-9
4-2
21-9
4-2
12
2
12
2
(
5
)In[]:=
ShowPlot[+5,{x,0,5},PlotRange->{{0,5},{0,30}},PlotLabel->"Figure 5.2.3",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large],Plot[6x-3,{x,0,5},PlotStyle->Directive[Orange]],ListPlot[{{2,9},{4,21}}],GraphicsText"y=6x-3",,2,Text"y=+5",,6,Text"(4,21)",,22,Text"(2,9)",,10
2
x
11
10
2
x
2
5
39
10
11
6
Out[]=

To demonstrate a secant line, we consider the single variable function in ().
f(x)=10(x-)sin(2x)
1
4
2
x
e
(
6
)We create a user-defined function to hold the function in (), assigned to the variable f below.
In[]:=
f[x_]:=10(x-)Sin[2x]
1
4
2
x
Figure 5.2.4 show the orange secant line between two points on the curve.
In[]:=
ManipulateShowPlot[f[x],{x,1,4},PlotLabel->"Figure 5.2.4",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large],Plot
,{x,1,4},PlotStyle->Directive[Orange],ListPlot[{{x1,f[x1]},{x2,f[x2]}},PlotStylePointSize[Large]],x1,,"",1,4,{{x2,2,""},1.1,4}
|
3
2
x
1
x
2
Out[]=
| |||||||||||
| |||||||||||
Problem 5.2.3 Calculate the function of the secant line to the curve of the function at =1 and =2.
g(x)
f(x)=+4
2
x
x
1
x
2
To solve this problem, we need to calculate and . We achieve this by creating a user-defined function f and the calculate =f(1) and =f(2).
y
1
y
2
y
1
y
2
In[]:=
f[x_]:=+4
2
x
In[]:=
f[1]
Out[]=
5
In[]:=
f[2]
Out[]=
8
The points are and . Now we can calculate the slope of using (3).
(,)=(1,5)
x
1
y
1
(,)=(2,8)
x
2
y
2
g
In[]:=
8-5
2-1
Out[]=
3
We have that the slope . If we use the point , we can use the point-slope form in (4) to calculate , shown in ().
m=3
(,)=(1,5)
x
1
y
1
g
y-=m(x-)y=m(x-)+y=g(x)=3(x-1)+5g(x)=3x-3+5g(x)=3x+2
y
1
x
1
x
1
y
1
(
7
)Figure 5.2.5 shows the curve in blue, the two points, and the secant line in orange.
f
In[]:=
ShowPlot[{+4,3x+2},{x,0,3},PlotLabel->"Figure 5.2.5",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large],ListPlot[{{1,5},{2,8}}],GraphicsText["(2,8)",{2,7}],Text"(1,5)",1,,Text"y=+4",,5,Text"y=3x+2",,9
2
x
17
4
2
x
1
4
11
4
Out[]=

As a ratio of to , the secant line of a single variable function can be seen as the average rate of change between two distinct points and on the curve of the function on the Cartesian plane.
Δy
Δx
f
(,)
x
1
y
2
(,)
x
2
y
2
5.3 Derivative
5.3 Derivative
We have to consider what happens to the secant line to a curve of a single variable function on the Cartesian plane when . Using the equation for the slope in (3), we would get the indeterminate form after substitution.
f
(,)=(,)
x
1
y
1
x
2
y
2
m
0
0
This reminds us of limits. We might consider the rise, , for an infinitesimally small run, . We could state that the run is from to as approaches , So the run from a point on the curve =x to a points =x+h=x+0=x approaches . We have that, - becomes and - becomes . We can now rewrite the equation for the slope as in (8).
Δy
Δx
x
x+h
h
0
x
1
x
2
0
y
2
y
1
f(x+h)-f(x)
x
2
x
1
(x+h)-x=h
m=
lim
h->0
f(x+h)-f(x)
h
(
8
)As an example, we consider . For we have . The slope of is calculated in (9) using (8).
f(x)=
2
x
f(x+h)
f(x+h)==+2xh+
2
(x+h)
2
x
2
h
m
f(x)
m=m=m=(2x+h)m=(2x)+(h)m=2x+0m=2x
lim
h->0
(+2xh+)-
2
x
2
h
2
x
h
lim
h->0
2xh+
2
h
h
lim
h->0
lim
h->0
lim
h->0
(
9
)In calculus we call the slope of a single variable function where , the instantaneous rate of change of the function at . The instantaneous rate of change (the slope at a specific point) is the derivative of the function at that point and is the slope of a tangent line to the curve at the point.
f
(,)=(,)
x
1
y
1
x
2
y
2
f
(,)=(,)
x
1
y
1
x
2
y
2
Definition 5.3.1 The first derivative of a single variable function at a point on the curve of the function is the slope of the tangent line to the curve at the point, as calculated in (8).
f(x)
Problem 5.3.1 Consider that time is represented by a value on the horizontal axis on the Cartesian plane. Researchers calculate the number of cases of a disease as represented by a value on the vertical axis of the Cartesian plane is given by the function in (10) on the interval . Calculate the average rate of change in the number of cases as goes from to and calculate the instantaneous rate of change in cases at the time when .
x
y
y=f(x)
x∈[5,10]
x
7
9
x=8
f(x)=+1
3
(x-3)
(
10
)We can create the function as a user-defined function f below.
In[]:=
f[x_]=+1
3
(x-3)
Out[]=
1+
3
(-3+x)
The Expand function show the polynomial expression on the right-hand side of the function.
In[]:=
Expand[f[x]]
Out[]=
-26+27x-9+
2
x
3
x
Figure 5.3.1 visualizes the number of cases.
In[]:=
Plot[f[x],{x,5,10},PlotLabel->"Figure 5.3.1",AxesLabel->{"Time as given by ","Number of cases as given by "},GridLines->Automatic,ImageSize->Large]
x
y
Out[]=

The average rate of change in the number of cases as goes from to is the slope of the secant line for the points where =7 and =9. We calculate and below.
x
7
9
x
1
x
2
y
1
y
2
In[]:=
f[7]
Out[]=
65
In[]:=
f[9]
Out[]=
217
The slope of this secant line between and is calculated below.
(7,65)
(9,217)
In[]:=
217-65
9-7
Out[]=
76
The average rate of the change in the number of cases between the time value and is cases.
x=7
x=9
76
We now use the definition of the derivative to calculate instantaneous rate of the change in cases at the time when . The calculations are shown in ().
x=8
m=m=m=m=m=m=(27-18x-9h+3+3h+)m=(27)+(-18x)+(-9)+(3)+(3h)+()m=27-18x+3
lim
h->0
f(x+h)-f(x)
h
lim
h->0
-26+27(x+h)-9+-(-26+27x-9+)
2
(x+h)
3
(x+h)
2
x
3
x
h
lim
h->0
-26+27x+27h-9(+2xh+)+(+3+3x+)+26-27x+9-
2
x
2
h
3
x
2
hx
2
h
3
h
2
x
3
x
h
lim
h->0
-26+27x+27h-9-18xh-9++3+3x++26-27x+9-
2
x
2
h
3
x
2
hx
2
h
3
h
2
x
3
x
h
lim
h->0
27h-18xh-9+3+3x+
2
h
2
hx
2
h
3
h
h
lim
h->0
2
x
2
h
lim
h->0
lim
h->0
lim
h->0
2
h
lim
h->0
2
x
lim
h->0
lim
h->0
2
h
2
x
(
11
)At we have the slope as shown in (12).
x=8
m=27-18(8)+3()m=27-144+192m=75
2
8
(
12
)The instantaneous change in the rate of infections at time is .
x=8
75
In the case of a polynomial, there is a much easier way to calculate the derivative than using Definition 5.3.1 and (8). For any term in the polynomial where ≠0 and , we have the derivate in (13), where the slope of the function is written as .
a
n
n
x
a
n
n≠0
m
f(x)
f'(x)
f(x)=m=f'(x)=n
a
n
n
x
a
n
n-1
x
(
13
)When we refer to the derivative of a function of a single variable , we state that we are taking the derivative of the function with respect to .
x
x
Problem 5.3.2 Calculate the first derivative of the function with respect to using (13).
f(x)=3
2
x
x
The solution is shown in (14).
f(x)=3f'(x)=(2×3)f'(x)=6f'(x)=6x
2
x
2-1
x
1
x
(
14
)
The pattern in (13) can be applied to polynomials with more terms.
Problem 5.3.3 Calculate the first derivative of the function .
f(x)=3+4+2x+3
3
x
2
x
The solution is shown in (15).
f(x)=3+4+2x+3f'(x)=(3×3)+(2×4)+(1×2)+(0×3)f'(x)=9+8x+2
3
x
2
x
3-1
x
2-1
x
1-1
x
0-1
x
2
x
(
15
)Note that ==1. Also note that the derivative of a constant (such as in this example) is since .
1-1
x
0
x
c
3
0
c=
0
cx
It is important to remember that fact that the derivative of a constant is as illustrated in Problem 5.3.3.
0
The D function in the Wolfram Language calculates derivatives. In the code cell below, we create the function in Problem 5.3.3 and assign it to the variable f.
In[]:=
f[x_]:=3+4+2x+3
3
x
2
x
The D function takes the function as first parameter and the variable with respect to which we are taking the derivative as second parameter.
In[]:=
D[f[x],x]
Out[]=
2+8x+9
2
x
The result is as we calculated in (15), albeit that the power of the variable is in ascending order.
Problem 5.3.4 Calculate the first derivative of function .
f(x)=-3x+2+
2
x
-1
x
We note the power in the last term. The result (for this term) would simple be . The Wolfram Language confirms the result below, where we pass the polynomial directly as first parameter.
-1
(-1×1)=-=-
-1-1
x
-2
x
1
2
x
In[]:=
D-3x+2+,x
2
x
1
x
Out[]=
-3-+2x
1
2
x
An important property of the derivative of a single variable function is that the derivative of the sum of terms is the sum of the derivative of the terms. This mean that we can recalculate the results of Problem 5.3.4 as in the code below.
In[]:=
D[,x]+D[-3x,x]+D[2,x]+D,x
2
x
1
x
Out[]=
-3-+2x
1
2
x
The result is exactly the same.
I the next example problem, we consider the first derivative of a function with roots.
Problem 5.3.5 Calculate the first derivative of the function .
f(x)=
5
4
x
To calculate the solution we have to remember that =. The result is shown in () and confirmed using code.
b
a
x
a
b
x
f(x)==f'(x)=×1-1f'(x)=-f'(x)=f'(x)=×f'(x)=
5
4
x
4
5
x
4
5
4
5
x
4
5
4
5
5
5
x
4
5
-
1
5
x
4
5
1
1
5
x
4
5
5
x
(
16
)Although the Wolfram Language displays the output differently, the results are in fact the same.
In[]:=
D,x
5
4
x
Out[]=
4
3
x
5
4/5
()
4
x
5.4 Derivatives of trigonometric functions
5.4 Derivatives of trigonometric functions
In our introduction to the derivative, we considered polynomials. There are many other types of single variable functions. In this section, we consider the derivatives on the sine, cosine, tangent, cosecant, secant, and cotangent functions.
We start with the sine function, shown in Figure 5.4.1.
In[]:=
Plot[Sin[x],{x,-2π,2π},PlotLabel->"Figure 5.4.1",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large]
Out[]=

We use the D function to calculate the derivative.
In[]:=
D[Sin[x],x]
Out[]=
Cos[x]
Figure 5.4.2 shows the sine function and its first derivative.
In[]:=
Plot[{Sin[x],Evaluate[D[Sin[x],x]]},{x,-2π,2π},PlotLabel->"Figure 5.4.2",PlotLegends->"Expressions",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large]
Out[]=
 |
|
In the code cells below, we calculate the first derivatives of the other five trigonometric functions and plot the functions and their derivatives.
D[Cos[x],x]
Out[]=
-Sin[x]
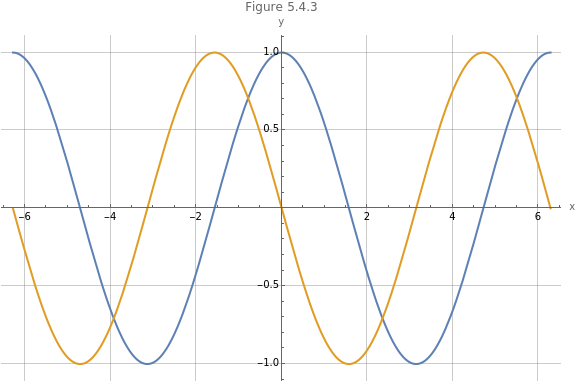
Figure 5.4.3 shows the cosine function and its first derivative.
In[]:=
Plot[{Cos[x],Evaluate[D[Cos[x],x]]},{x,-2π,2π},PlotLabel->"Figure 5.4.3",PlotLegends->"Expressions",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large]
Out[]=
 |
|
In[]:=
D[Tan[x],x]
Out[]=
2
Sec[x]
Figure 5.4.4 shows the tangent function and its first derivative.
In[]:=
Plot[{Tan[x],Evaluate[D[Tan[x],x]]},{x,-2π,2π},PlotLabel->"Figure 5.4.4",PlotLegends->"Expressions",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large]
Out[]=
 |
|
In[]:=
D[Csc[x],x]
Out[]=
-Cot[x]Csc[x]
Figure 5.4.5 shows the cosecant function and its first derivative.
In[]:=
Plot[{Csc[x],Evaluate[D[Csc[x],x]]},{x,-2π,2π},PlotLabel->"Figure 5.4.5",PlotLegends->"Expressions",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large]
Out[]=
 |
|
In[]:=
D[Sec[x],x]
Out[]=
Sec[x]Tan[x]
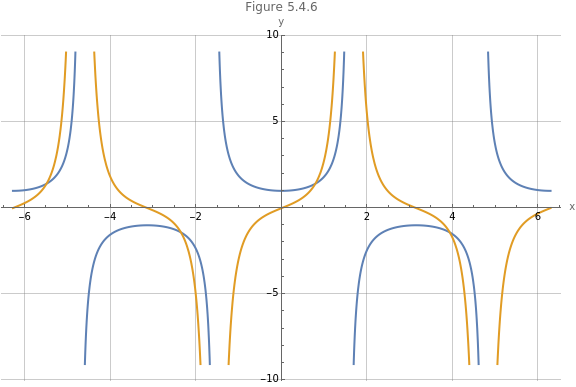
Figure 5.4.6 shows the secant function and its first derivative.
In[]:=
Plot[{Sec[x],Evaluate[D[Sec[x],x]]},{x,-2π,2π},PlotLabel->"Figure 5.4.6",PlotLegends->"Expressions",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large]
Out[]=
 |
|
In[]:=
D[Cot[x],x]
Out[]=
-
2
Csc[x]
Figure 5.4.7 shows the cotangent function and its first derivative.
In[]:=
Plot[{Cot[x],Evaluate[D[Cot[x],x]]},{x,-2π,2π},PlotLabel->"Figure 5.4.7",PlotLegends->"Expressions",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large]
Out[]=
 |
|
5.5 Derivatives of exponential and logarithm functions
5.5 Derivatives of exponential and logarithm functions
The exponential function and the natural logarithm are two very commonly used functions. In fact, we term any function that has teh unknown as the power and an exponential function. The first derivative of with respect to is unique. We use the D function to calculate the derivative.
x
e
x
e
x
In[]:=
D[,x]
x
Out[]=
x
We note that the first derivative is the function itself.
We calculate the first derivative of the natural log with respect to below.
x
In[]:=
D[Log[x],x]
Out[]=
1
x
By the properties of logarithms we have that . This property allows us to solve more difficult functions that we will explore in chapter 8.
5.6 Notation
5.6 Notation
The are various notations used for the derivate. We have already seen that the first derivative of the function with respect to is written as . This notation is termed the Newton notation.
f(x)
x
f'(x)
As alternative we have the Leibniz notation in (17).
f'(x)==f=f(x)
df
dx
d
dx
d
dx
(
17
)Here, the , refers to a small the terms a small change in. If we write , then we can also use the Leibniz notation in (18).
d
y=f(x)
dy
dx
(
18
)Some mathematicians also use the notation in (19).
Df
x
D
x
(
19
)In[]:=
Plot[2RealAbs[x],{x,-1,1}]
Out[]=

In[]:=
D[RealAbs[x],x]/.x->0
Out[]=
Indeterminate
2
1
3
x
2
3
x
(
20
)In[]:=
CubeRoot[x]/.x->{-1,1}
Out[]=
{-1,1}
In[]:=
Plot[CubeRoot[x],{x,-2,2}]
Out[]=

In[]:=
D[CubeRoot[x],x]
Out[]=
1
3
2
3
x
In[]:=
Limit[D[CubeRoot[x],x],x->0,Direction->"FromBelow"]
Out[]=
∞
In[]:=
Limit[D[CubeRoot[x],x],x->0,Direction->"FromAbove"]
Out[]=
∞
In[]:=
2
3
(-1)
Out[]=
-0.5+0.866025
In[]:=
Plot,{x,0.0001,1}
1
3
2
3
x
Out[]=

In[]:=
f[x_]:=
|
In[]:=
Plot[f[x],{x,-2,2}]
Out[]=

In[]:=
D[+1,x]
2
x
Out[]=
2x
In[]:=
D[--1,x]
2
x
Out[]=
-2x
In[]:=
fPrime[x_]:=
|
|
In[]:=
Plot[{f[x],fPrime[x]},{x,-1,1}]
Out[]=

In[]:=
D[f[x],x]/.x->0
Out[]=
Indeterminate
