4 | LIMITS AND CONTINUITY
4 | LIMITS AND CONTINUITY
This chapter of Single Variable Calculus by Dr JH Klopper is licensed under an Attribution-NonCommercial-NoDerivatives 4.0 International Licence available at http://creativecommons.org/licenses/by-nc-nd/4.0/?ref=chooser-v1 .
4.1 Introduction
4.1 Introduction
Limits play a crucial role in differentiation and integration. In the differentiation of a single variable function, , we consider the change in for a difference in that, for the latter, in the limit, approaches . In integration, we consider the sum over rectangles that in the limit approaches a base (width) of .
y=f(x)
y
x
0
0
We will develop these concepts a bit later. For now we occupy our minds with a function and the value that approaches as approaches some value . We do examine this limit as approaches from above and below . In the next section, we explore what the terms approaching and limit actually mean.
y=f(x)
y
x
a
x
a
x=a
In some of our exploration in this chapter, we will make use of visualization (plotting) to help us understand the limits. We cannot plot an infinitely large plot and although plotting is helpful, we must not rely on it at all times. Curves of functions can have unexpected behaviour outside our intervals of plotting.
4.2 The limit of a linear function
4.2 The limit of a linear function
Definition 4.2.1 A linear function in a single variable has the form .
y=mx+b
We note from the definition that a linear function is the equation for a straight line in the plane, with a slope, , and a -intercept, .
m
y
b
Our example function is . We let , where and explore the values of as the values of get closer and closer to . We start creating the function in the Wolfram Language and assign it to the variable f.
f(x)3x+2
xa
a1
y
x
a1
f[x_]:=3x+2(*Createthefunctionfthattakesasingleparameterx*)
We can generate a table of values of as gets closer and closer to from the negative -axis towards . Below, we use the TableForm function and pass the Table function as parameter. The first parameter of the Table function is a list of values for . The second parameter is a counter that changes the values of from to in steps of .
y
x
x1
x
x=1
(x,y)
x
0.9
0.99
0.01
TableForm[Table[{x,f[x]},{x,0.9,0.99,0.01}]](*Tableofinputandoutputvaluesforthefunctionf*)
Out[]//TableForm=
0.9 | 4.7 |
0.91 | 4.73 |
0.92 | 4.76 |
0.93 | 4.79 |
0.94 | 4.82 |
0.95 | 4.85 |
0.96 | 4.88 |
0.97 | 4.91 |
0.98 | 4.94 |
0.99 | 4.97 |
It seems that as approaches we have that approaches (gets closer and closer to ). We can also look at the values of as approaches from the positive infinity side.
x
1
y
5
5
y
x
1
TableForm[Table[{x,f[x]},{x,1.1,1.01,-0.01}]](*Tableofinputandoutputvaluesforthefunctionf*)
Out[]//TableForm=
1.1 | 5.3 |
1.09 | 5.27 |
1.08 | 5.24 |
1.07 | 5.21 |
1.06 | 5.18 |
1.05 | 5.15 |
1.04 | 5.12 |
1.03 | 5.09 |
1.02 | 5.06 |
1.01 | 5.03 |
Once again, it seems that as we get closer to (from above) we have that approaches .
x=1
y
5
In the case of our example we can also consider the value of when is exactly . We pass the value as parameter to the self-created function f.
y
x
1
1
f[1](*Calculatethevalueofywhenxis1*)
Out[]=
5
Figure 4.2.1 shows the limit of as approaches .
f(x)=3x+2
x
1
Show[Plot[3x+2,{x,-1,2},PlotLabel->"Figure 4.2.1",ImageSize->Large,AxesLabel->{"x","y"},GridLines->Automatic],ListPlot[{{1,5}}]]
Out[]=

As expected, we have that the value of as approaches . We say that a limit exists if the value that the function approaches from above and below are both . We use the notation f(x) for the limit from the negative infinity (below) side of and the notation f(x) for the limit from the positive infinity (above) side. These are termed left- and right-hand side limits.
y=5
x
1
L
L
lim
x->
-
a
x=a
lim
x->
+
a
Definition 4.2.2 A limit of a function exists and is if (1) holds.
y=f(x)
L
lim
x->a
lim
x->
-
a
lim
x->
+
a
(
1
)The left- and right-hand limits have to exist and be equal to each other. Note that we still have a limit even if the function is not defined at or takes on a value other than at . The next two examples demonstrate.
x=a
L
x=a
In (2), we define a function that is not defined at .
x=1
f=
|
|
(
2
)In Figure 4.2.2 we note the non-existence of a value for when as visualized by the open marker. The function is said to be discontinuous at .
y
x=1
x=1
In[]:=
Show[Plot[3x+2,{x,0.9,0.999},PlotLabel->"Figure 4.2.2",ImageSize->Large,AxesLabel->{"x","y"},GridLines->Automatic,PlotRange->{{0.9,1.1},{4,6}}],Plot[3x+2,{x,1.001,1.1},PlotRange->{{0.9,1.1},{4,6}}],ListPlot[{{1,5}},PlotMarkers->"OpenMarkers"]]
Out[]=

The limit as approaches is still , though. We state this because still clearly gets closer-and-closer to as approaches from both below and above.
x
1
5
y
5
x
1
In (3), we see another discontinuity.
f=
|
|
(
3
)The function is visualized in Figure 4.2.3.
Show[Plot[3x+2,{x,0.9,0.999},PlotLabel->"Figure 4.2.3",ImageSize->Large,AxesLabel->{"x","y"},GridLines->Automatic,PlotRange->{{0.9,1.1},{4,6}}],Plot[3x+2,{x,1.001,1.1},PlotRange->{{0.9,1.1},{4,6}}],ListPlot[{{1,5}},PlotMarkers->"OpenMarkers"],ListPlot[{{1,4.5}}]]
Out[]=

The limit is still as approaches , because this is the values that approaches as approaches from both sides.
5
x
1
y=f(x)
x
1
When Definition 4.2.2 does not hold, we may still have one-sided limits. Consider the function in (4).
f(x)=
|
|
(
4
)Figure 4.2.4 visualizes the function.
Show[Plot[x,{x,-1,1},PlotLabel->"Figure 4.2.4",ImageSize->Large,AxesLabel->{"x","y"},GridLines->Automatic,PlotRange->{{-1,3},{-1,2}}],Plot[x-1,{x,1.001,4},PlotRange->{{-1,3},{-1,2}}],ListPlot[{{1,0}},PlotMarkers->"OpenMarkers"],ListPlot[{{1,1}}]]
Out[]=

The limit as approaches does not exist. One-sided limits do exist, but they are not the same for this discontinuous function. The one-sided limits are shown in (5).
x
1
lim
x->1
lim
x->
-
1
lim
x->
+
1
(
5
)
Homework 4.2.1 Calculate the limit of the function as approaches .
4.3 Asymptotes
4.3 Asymptotes
Definition 4.3.1 An asymptote is a virtual line (vertical , horizontal, oblique, or curvilinear) that a function approaches but does not reach as the function heads to infinity or some other value.
The function in (6) has a vertical and a horizontal asymptote.
f(x)=
1
x
(
6
)Figure 4.3.1 shows the function.
In[]:=
Plot,{x,-20,20},PlotLabel->"Figure 4.3.1",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large,PlotRange->{{-20,20},{-20,20}}
1
x
Out[]=

We note some important limits in (7) where is a finite real number.
lim
x->∞
a
x
lim
x->-∞
a
x
lim
x->
-
0
a
x
lim
x->
+
0
a
x
(
7
)As approaches either negative or positive infinity, we note that approaches . As approaches from the left-hand side, we have that approaches and as approaches from the right-hand side, we have that approaches . We say that there is a vertical asymptote at and there is a horizontal asymptote at .
0
0
1
Problem 4.3.1 Calculate the asymptotes of the function in (8).
f(x)=
(x+2)(x-5)
(x-3)(x+1)
(
8
)We plot the function in Figure 4.3.2.
Plot,{x,-8,8},PlotLabel->"Figure 4.3.2",GridLines->{Range[-8,8,1],Range[-5,8,1]},AxesLabel->{"x","y"},ImageSize->Large
(x+2)(x-5)
(x-3)(x+1)
Out[]=

Since we cannot divide by , we have that the function is undefined when or . These are the vertical asymptotes. We can use the Limit function to confirm these asymptotes. The Direction keyword parameter can be used to indicate if we approach a values from the left (below) (“FromBelow”) or the right (above) (“FromAbove”).
0
x=3
x=-1
In[]:=
Limit,x->-1,Direction->"FromBelow"
(x+2)(x-5)
(x-3)(x+1)
Out[]=
-∞
In[]:=
Limit,x->-1,Direction->"FromAbove"
(x+2)(x-5)
(x-3)(x+1)
Out[]=
∞
In[]:=
Limit,x->3,Direction->"FromBelow"
(x+2)(x-5)
(x-3)(x+1)
Out[]=
∞
In[]:=
Limit,x->3,Direction->"FromAbove"
(x+2)(x-5)
(x-3)(x+1)
Out[]=
-∞
There is also a horizontal asymptote at . We use the and as .
y=1
Limit
function again to determine the limit of the function as In[]:=
Limit,x->∞
(x+2)(x-5)
(x-3)(x+1)
Out[]=
1
In[]:=
Limit,x->-∞
(x+2)(x-5)
(x-3)(x+1)
Out[]=
1
Problem 4.3.2 Calculate the asymptotes of the function in (9).
f(x)=
2+3x+1
2
x
x+2
(
9
)We plot the function in Figure 4.3.3 and show the oblique asymptote as a dashed line.
ShowPlot,{x,-4,2},PlotLabel->"Figure 4.3.3",GridLines->{Range[-4,4,1],Range[-30,20,5]},AxesLabel->{"x","y"},ImageSize->Large,Plot[2x-1,{x,-4,2},PlotStyle->{Automatic,Dashed}]
2+3x+1
2
x
x+2
Out[]=

Using long division, we find that the result in (10).
f(x)=2x-1+
3
x+2
(
10
)The FullSimplify function returns the result of long division.
In[]:=
FullSimplify
2+3x+1
2
x
x+2
Out[]=
-1+2x+
3
2+x
As approaches negative and positive infinity, we have that the remainder (the fraction in (10)) approaches the value and we are left with , which is the oblique asymptote.
0
f(x)=2x-1
Homework 4.3.1 Calculate the equation for the asymptote in (11).
f(x)=
2+3x+2
2
x
x+1
(
11
)
Problem 4.3.3
The function in (12) is termed to have a curvilinear asymptote as approaches negative and positive infinity. The function is plotted in Figure 4.3.4.
x
f(x)=x+sin(x)
(
12
)Plot[x+Sin[x],{x,-10π,10π},PlotLabel->"Figure 4.3.4",AxesLabel->{"x","y"},ImageSize->Large,GridLines->Automatic]
Out[]=

4.4 Limits and continuity
4.4 Limits and continuity
Here, we consider ourselves with a function that takes as input a subset of and produces an output that is in . Now we can use our understanding of a limit to define what it is for a function to be continuous for all the values in the subset of .
f
Definition 3.4.1 A function in a single variable is continuous on an interval that is a subset of containing the value if the following three assumptions are met.
1. The limit of exists at 2. The function is defined at , in other words, exists3. The limit of as approaches is equal to , written in (13)
lim
x->c
(
13
)Remember that the continuity of a function is very much determined by its domain. A function that is not continuous for all may be continuous on some interval in .
The function plotted in Figure 4.2.1 is continues for all values of . The function plotted in Figure 4.2.2 and in Figure 4.2.3 are not continuous for all values of . They are continuous if we specify a domain such as , though.
Problem 4.4.1 Determine if the function in (14) is continuous for all values of .
x
f(x)=|x|
(
14
)Figure 4.4.1 is a graph of the function.
In[]:=
Plot[Abs[x],{x,-3,3},ImageSize->Large,GridLines->Automatic,PlotLabel->"Figure 4.4.1"]
Out[]=

We note that all three assumptions for the definition of a continuous function are met with respect of the domain and the function.
x∈(-∞,∞)
Homework 4.4.1 Determine if the function in (15) is continuous on the interval .
f(x)=+1
2
x
x+3
(
15
)
4.5 Evaluating limits using algebraic techniques
4.5 Evaluating limits using algebraic techniques
As limits are at the heart of calculus, we should develop approaches to solve limit problems. We start by examining commonly encountered limits.
4.5.1 Limits to memorize
4.5.1 Limits to memorize
There are some limits that are so useful that it is probably good just to memorize them. The first in this set is the simple hyperbola in (16).
f(x)=
1
x
(
16
)We have encountered a hyperbola in the section on asymptotes. Figure 4.5.1.1 visualizes the limit of (16) as approaches from the left and the right.
x
0
In[]:=
Plot,{x,-1,1},PlotLabel->"Figure 4.5.1.1",GridLines->Automatic,AxesLabel->{"x","y"},ImageSize->Large,PlotRange->{{-1,1},{-100,100}}
1
x
Out[]=

The approaches from the left (below) and from the right (above). We use the
Limit
function used in the code cells below confirms our visual interpretation of the limit as 0
Direction
keyword parameter to set the direction of the limit.In[]:=
Limit,x->0,Direction->"FromBelow"
1
x
Out[]=
-∞
In[]:=
Limit,x->0,Direction->"FromAbove"
1
x
Out[]=
∞
From these results we write the limits in (17).
lim
x->
-
0
1
x
lim
x->
+
0
1
x
(
17
)We have a vertical asymptote at . There is also a horizontal asymptote at . This limit calculated as approaches negative and positive infinity.
x=0
y=0
x
In[]:=
Limit,x->-∞
1
x
Out[]=
0
In[]:=
Limit,x->∞
1
x
Out[]=
0
From the results, we would write (18).
lim
x->-∞
1
x
lim
x->∞
1
x
(
18
)The next function in this set for which we want to calculate a limit, is shown in (19).
f(x)=sin
(x)
x
(
19
)Figure 4.5.1.2 visualizes the function.
Plot,{x,-4π,4π},PlotLabel->"Figure 4.5.1.2",AxesLabel->{"x","y"},ImageSize->Large,GridLines->Automatic
Sin[x]
x
Out[]=
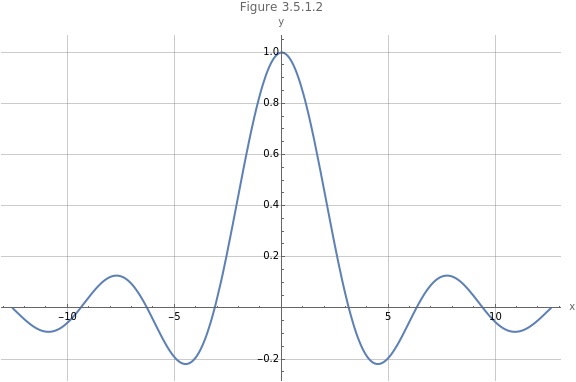
The code below confirms that the limit is .
1.0
In[]:=
Limit,x->0
Sin[x]
x
Out[]=
1
We write the result in (20) . Note that by omitting the direction in the notation used in (20), we state that the left- and right-hand side limits exists and are the same and that we have a true limit, as opposed to one-sided limits.
lim
x->0
sin(x)
x
(
20
)The next limit in the set involves the cosine function, shown in (21).
f(x)=
cos(x)-1
x
(
21
)Figure 4.5.1.3 visualizes the limit.
Plot,{x,-2π,2π},PlotLabel->"Figure 4.5.1.3",AxesLabel->{"x","y"},ImageSize->Large,GridLines->Automatic
Cos[x]-1
x
Out[]=

In[]:=
Limit,x->0
Cos[x]-1
x
Out[]=
0
The final limit in this series is the famous number , shown in (21).
e
f(x)=
x
1+
1
x
(
22
)Figure 4.5.1.4 shows that the limit as approaches infinity is .
x
e≈2.718
Plot,{x,1,10},PlotLabel->"Figure 4.5.1.4",AxesLabel->{"x","y"},ImageSize->Large,GridLines->Automatic
x
1+
1
x
Out[]=

The Limit function confirms the result.
In[]:=
Limit,x->∞
x
1+
1
x
Out[]=
The Wolfram Language prints the character which denotes Euler’s number .
e
We write the result as in (23).
lim
x->∞
x
1+
1
x
(
23
)We use the N function to print a numerical approximation of .
N[,10](*Numericalapproximationwithatotalof10digits*)
Out[]=
2.718281828
4.5.2 Limits by substitution
4.5.2 Limits by substitution
In the section of linear functions, we examined limits that can be calculate by simple substitution. The value of a function exists at and is simply .
x=c
Problem 4.5.2.1 Calculate the limit of the function in (24) and determine the limit as approaches .
lim
x->π
(
24
)To calculate the limit, we simply substitute .
Sin[π](*Calculatethesineofπ*)
Out[]=
0
The Limit function confirms the result.
In[]:=
Limit[Sin[x],x->π]
Out[]=
0
Figure 4.5.2.1 visualizes the limit.
ShowPlotSin[x],{x,0,2π},PlotLabel->"Figure 4.5.2.1",AxesLabel->{"x","y"},GridLines->Range0,2π,,Range-1,1,,ImageSize->Large,TicksRange0,2π,,{-1,0,1},ListPlot[{{π,0}}]
π
4
1
2
π
4
Out[]=

The problem was solve by simple substitution.
Homework 4.5.2.1 Calculate the limit of the function as approaches
4.5.3 Limits by factoring
4.5.3 Limits by factoring
Following the limits that we can simply recall from memory and limits that can be solved by direct substitution, we consider our second technique for finding limits. Some functions contain expressions that are amenable to factoring. Consider the function in (25).
f(x)=-25
2
x
x-5
(
25
)The function in (25) has a discontinuity at , since the function is note defined at (resulting in division by ). By factoring the denominator where , we have common factors in the numerator and in the denominator that can be cancelled. This problem is an example of a function containing a removable discontinuity.
0
The removable discontinuity is visualized in Figure 4.5.3.1.
ShowPlot-25,{x,3,4.99},PlotLabel->"Figure 4.5.3.1",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large,PlotRange->{{3,7},{8,12}},Plot-25,{x,5.01,7},PlotRange->{{3,7},{8,12}},ListPlot[{{5,10}},PlotMarkers->"OpenMarkers"]
2
x
x-5
2
x
x-5
Out[]=

The limit is calculated in (26) and confirmed with code.
lim
x->5
2
x
x-5
lim
x->5
(x-5)(x+5)
x-5
lim
x->5
(
26
)In[]:=
Limit-25,x->5
2
x
x-5
Out[]=
10
The final solution is showed in (27).
lim
x->5
2
x
x-5
(
27
)We visualize the result in Figure 4.5.3.2.
ShowPlot-25,{x,3,7},PlotLabel->"Figure 4.5.3.2",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large,ListPlot[{{5,10}}]
2
x
x-5
Out[]=

4.5.4 Limits by conjugate multiplication
4.5.4 Limits by conjugate multiplication
Another technique that is often used in solving algebraic problems is conjugate multiplication. Conjugate multiplication is particularly useful when dealing with square roots.
Problem 4.5.4.1 Calculate the limit in (28).
lim
x->4
x
-2x-4
(
28
)The function has a removable discontinuity at . The conjugate of is . We use this in conjugate multiplication in (29).
x=4
x
-2x
+2lim
x->4
x
-2x-4
x
+2x
+2lim
x->4
x-4
(x-4)(
x
+2))lim
x->4
1
x
+2(
29
)Now we can use simple substitution to calculate the limit (assuming that as shown in (28).
4
=+2lim
x->4
1
x
+2lim
x->4
1
4
+2lim
x->4
1
2+2
1
4
(
30
)The Limit function confirms the result.
In[]:=
Limit,x->4
x
-2x-4
Out[]=
1
4
Homework 4.5.4.1 Calculate the limit in (31).
lim
x->9
x
-3x-9
(
31
)
4.5.5 Limits at infinity with polynomial fractions
4.5.5 Limits at infinity with polynomial fractions
The limits of expressions with a polynomial in the numerator and in the denominator can take three different forms. In the first, the degree of the polynomials are the same in both the numerator an in the denominator.
Problem 4.5.5.1 Calculate the limit in (32), where the degree of the polynomials in the numerator and the denominator are the same.
lim
x->∞
4+2x
3
x
2+-2x-1
3
x
2
x
(
32
)As the value of increases towards infinity, is should be clear that it is the highest power of that increases the most. This happens so much so that the other powers of are dwarfed by the value of the highest power of . As approaches infinity it is only these powers that remain and we have the solution in (33).
x
lim
x->∞
4+2x
3
x
2+-2x-1
3
x
2
x
lim
x->∞
4
3
x
2
3
x
lim
x->∞
4
2
4
2
(
33
)If we instead used substitution as our initial step, we would calculate the limit to be . This is not and actually tells use nothing about the limit. Instead, we have to follow the reasoning set forth above. We confirm the result with code.
1
In[]:=
Limit,x->∞
4+2x
3
x
2+-2x-1
3
x
2
x
Out[]=
2
Homework 4.5.5.1 Calculate the limit in (34).
lim
x->∞
3+2-3x+5
3
x
2
x
6-2
3
x
(
34
)
In the second case, we have that the degree of the polynomial in the numerator is higher than the degree of the polynomial in the denominator.
Problem 4.5.5.2 Calculate the limit in (35).
lim
x->∞
2
x
x+3
(
35
)In this case the value of the numerator grow much faster than the denominator and the value of the function increases without limit. We use code to calculate the solution.
In[]:=
Limit,x->∞
2
x
x+3
Out[]=
∞
The Wolfram Language returns a result of . Note that is not a specific value and we state that the limit does not exist.
∞
∞
Homework 4.5.5.2 Calculate the limit in (36).
lim
x->∞
3+2-3x+5
3
x
2
x
6
2
x
(
36
)
In the last case, we have a greater degree polynomial in the denominator. In this case, the limit is always . The value in the denominator increase much more than that in the numerator. As approaches infinity, we have the familiar limit in Section 4.3.
0
Problem 4.5.5.3 Calculate the limit in (37).
lim
x->∞
2
x
3
x
2
x
(
37
)As approaches infinity we have the limit in (38).
x
lim
x->∞
1
x
(
38
)The code below confirms the result.
In[]:=
Limit-25+3+3x+1,x->∞
2
x
3
x
2
x
Out[]=
0
Homework 4.5.5.3 Calculate the limit in (39).
lim
x->∞
3+2-3x+5
3
x
2
x
6
4
x
(
39
)
4.5.6 Limit by other algebraic techniques
4.5.6 Limit by other algebraic techniques
There are many techniques that are explored in a course on algebra.
Problem 4.5.6.1 Calculate the limit in (40).
lim
x->0
1
x+4
1
4
x
(
40
)Using Wolfram Language code, we see that the limit does indeed exist.
In[]:=
Limit-,x->0
1
x+4
1
4
x
Out[]=
-
1
16
We explore one way to solve our algebraic dilemma in (41).
lim
x->0
1
x+4
1
4
x
lim
x->0
4-(x+4)
4(x+4)
x
lim
x->0
-x
4(x+4)
x
x+4
x+4
x+4
x+4
lim
x->0
-x
4
x
1
x+4
lim
x->0
-1
4
1
1
x+4
lim
x->0
-1
4(x+4)
-1
4(0+4)
-1
16
(
41
)
4.6 Evaluating indeterminate limits
4.6 Evaluating indeterminate limits
Definition 4.6.1 Limits that result in the values in (42) are in indeterminate form.
±,,0×(±∞),∞-∞,
∞
∞
0
0
0
0
(
42
)We have already examined the first indeterminate form in (33), when we examined fractions of polynomials with similar degree in the numerator and denominator. Examples of the indeterminate forms are explored below. We will examine methods to solve these problems in the next section.
Problem 4.6.1 Calculate the limit in (43).
lim
x->∞
x
e
x
(
43
)Substitution results in the indeterminate form shown in (44).
lim
x->∞
x
e
x
∞
e
∞
∞
∞
(
44
)Using the Limit function, we see that the limit does not exist (the result is ).
∞
In[]:=
Limit,x->∞
x
x
Out[]=
∞
Note that is not equal to or to . Direct substitution yields an indeterminate form. Figure 4.6.1 visualizes the problem. Its shows the value of the function increasing as increases. No specific value, , is reached. We will need another technique to calculate the result, though.
x
L
Plot,{x,2,10},PlotLabel->"Figure 4.6.1",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large
x
x
Out[]=

Problem 4.6.2 Calculate the limit in (45).
lim
x->0
x
e
x
(
45
)Direct substitution yields the indeterminate form in (46).
lim
x->0
x
e
x
0
e
0
1-1
0
0
0
(
46
)Using the Limit function, we see an unexpected result.
In[]:=
Limit-1,x->0
x
x
Out[]=
1
Figure 4.6.2 visualizes the problem.
Plot-1,{x,-1,2},PlotLabel->"Figure 4.6.2",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large
x
x
Out[]=

As with the Problem 4.6.1 we will need another technique to solve this problem.
Problem 4.6.3 Calculate the limit in (47).
lim
x->
+
0
(
47
)Direct substitution results in (48).
lim
x->
+
0
(
48
)Figure 4.6.3 is a reminder that the natural log is not defined for non-positive real number and approaches as approaches from above.
-∞
0
Plot[Log[x],{x,-1,10},PlotLabel->"Figure 4.6.3",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large]
Out[]=

Using the Limit function, we see that a limit does exist.
In[]:=
Limit[xLog[x],x->0,Direction->"FromAbove"]
Out[]=
0
Yet again, we will require a new technique to solve this problem.
Problem 4.6.4 Calculate the limit in (49).
lim
x->∞
x
e
(
49
)Direct substitution results in (50).
lim
x->∞
x
e
(
50
)Note that . Using the
Limit
function shows that the limit does not exist.In[]:=
Limit[x-,x->∞]
x
Out[]=
-∞
Figure 4.6.4 shows why the limit does not exist.
In[]:=
Plot[x-,{x,2,4},PlotLabel->"Figure 3.6.4",AxesLabel->{"x","y"},GridLines->Automatic,ImageSize->Large]
x
Out[]=

As with all the problems in this section, we will require a new technique to solve this problem.
Problem 4.6.5 Calculate the limit in (51).
lim
x->0
x
x
(
51
)Direct substitution results in (52).
lim
x->0
x
x
0
0
(
52
)Using the Limit function, we see an unexpected result.
In[]:=
Limit[,x->0]
x
x
Out[]=
1
Below, we use the and as approaches from above and below.
Table
function to create a table of values for 0
In[]:=
TableForm[Table[{x,},{x,0.0001,0.00001,-0.00001}]]
x
x
Out[]//TableForm=
0.0001 | 0.999079 |
0.00009 | 0.999162 |
0.00008 | 0.999246 |
0.00007 | 0.999331 |
0.00006 | 0.999417 |
0.00005 | 0.999505 |
0.00004 | 0.999595 |
0.00003 | 0.999688 |
0.00002 | 0.999784 |
0.00001 | 0.999885 |
In[]:=
TableForm[Table[{x,Re[]},{x,-0.0001,-0.00001,0.00001}]]
x
x
Out[]//TableForm=
-0.0001 | 1.00092 |
-0.00009 | 1.00084 |
-0.00008 | 1.00075 |
-0.00007 | 1.00067 |
-0.00006 | 1.00058 |
-0.00005 | 1.0005 |
-0.00004 | 1.00041 |
-0.00003 | 1.00031 |
-0.00002 | 1.00022 |
-0.00001 | 1.00012 |
In both cases, we see the solution approaching .
In the next section, we explore a method to solve some indeterminate forms.
4.7 L’Hôpital’s rule
4.7 L’Hôpital’s rule
Guillaume de l’Hôpital developed a mathematical theorem in the late seventeenth century that can be used to calculate some limit that are in indeterminate form.
Theorem 4.7.1 L’Hôpital’s rule states that if the limit of the ratio of two functions, and , as approaches a certain value is in an indeterminate form, and if the derivatives of the numerator and denominator exist in a neighborhood of that value (except possibly at that value itself), then the limit of the ratio is equal to the limit of the ratio of their derivatives.
We can write the first derivate of a function with respect to as . We see L’Hôpital’s rule in (53).
lim
x->c
f(x)
g(x)
lim
x->c
f'(x)
g'(x)
(
53
)
Problem 4.7.1 Calculate the limit in (54).
lim
x->0
sin(x)
x
(
54
)We have explored this limit before and know that it is as approaches .
1
0
Direct substitution results in an indeterminate form. We recognize a ratio of the functions and in this limit problem and consider using L’Hôpital’s rule.
We have not considered derivatives yet. Instead, we use the .
D
function here to calculate the derivative of both the numerator and the denominator with respect to the variable In[]:=
D[Sin[x],x]
Out[]=
Cos[x]
The first derivative of with respect to is . We do the same for the denominator.
In[]:=
D[x,x]
Out[]=
1
The derivative of with respect to is . We can now rewrite the limit as in (55).
1
lim
x->0
sin(x)
x
lim
x->0
cos(x)
1
cos(0)
1
1
1
(
55
)
In some cases we might have to apply L’Hôpital’s rule more than once.
Problem 4.7.2 Calculate the limit in (56).
lim
x->∞
2
x
-x
e
1+
-x
e
(
56
)In[]:=
Limit,x->∞
2
x
-x
1+
-x
Out[]=
0
Direct substitution results in an indeterminate form. We calculate the first derivatives below.
In[]:=
D[,x]
2
x
-x
Out[]=
2x-
-x
-x
2
x
In[]:=
D[1+,x]
-x
Out[]=
-
-x
We have the new limit in (57).
lim
x->∞
2-
-x
xe
2
x
-x
e
-
-x
e
lim
x->∞
-2x-
2
x
1
(
57
)Direct substitution results in an indeterminate form again. We apply L’Hôpital’s rule again. To take a second derivative, we pass the parameter twice.
In[]:=
D[,x,x]
2
x
-x
Out[]=
2-4x+
-x
-x
-x
2
x
In[]:=
D[1+,x,x]
-x
Out[]=
-x
The limit can now be calculated as shown in (58).
lim
x->∞
2-4+
-x
e
-x
xe
2
x
-x
e
-x
e
lim
x->∞
2
x
lim
x->∞
2
x
lim
x->∞
2
(x-2)
lim
x->∞
(
58
)
Homework 4.7.1 Use the Wolfram Language D function to calculate the derivatives to solve the limit in (59).
lim
x->∞
x
e
2
x
(
59
)