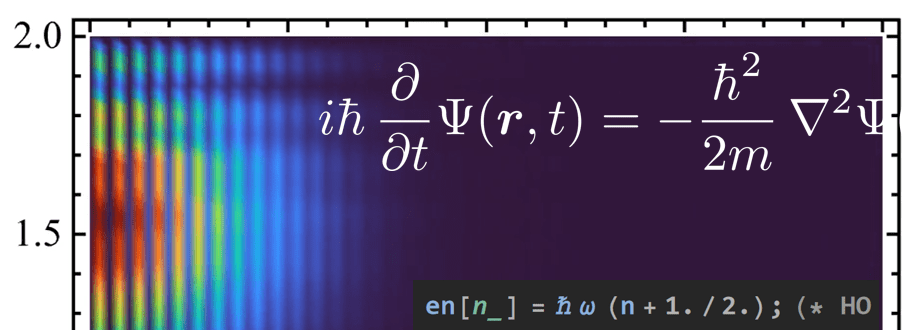Gaussian Wave Packet in Free Space

The Gaussian wave packet with zero potential is maybe the most fundamental model of a quantum mechanical particle propagating in free space. The general property of such a wave packet is shown below:

A wave packet with non-zero momentum at t=0. The maximum of the probability density $\rho=|\Psi|^2$ coincides with a zero of the imaginary part, Im $\Psi(x)=0$ at $x=0$ .

A wave packet with non-zero momentum at t=0. The maximum of the probability density $\rho=|\Psi|^2$ coincides with a zero of the imaginary part, Im $\Psi(x)=0$ at $x=0$ .

What makes the wave packet travel to the right is the initial condition, i.e., the wave packet at $t=0$ , being complex-valued and not real. Indeed, it can be shown that if one applies the operator $e^{i p\,x_\text{op}/\hbar}$ to a wave function, the expectation value of its momentum is increased by $p$ . In position space, this operator is simply the multiplicative factor $e^{i p x/\hbar}$ . In the current example, the momentum of the wave packet was zero before multiplication with this factor, so the wave packet after "hitting" it with the operator made became complex with an expectation value for the momentum $\langle p\rangle=p>0$ .

The movement of the wave packet can be illustrated as follows:

Real, imaginary and absolute value-squared of a Gaussian wave packet traveling to the right. The black vertical line shows the position of the maximum of $|\Psi|^2$ , associated with the group velocity. The thick and thin blue dashed vertical lines approximately show different zeros of the imaginary part, Im $\Psi(x)=0$ . They are associated with the phase velocity.

Real, imaginary and absolute value-squared of a Gaussian wave packet traveling to the right. The black vertical line shows the position of the maximum of $|\Psi|^2$ , associated with the group velocity. The thick and thin blue dashed vertical lines approximately show different zeros of the imaginary part, Im $\Psi(x)=0$ . They are associated with the phase velocity.

As the figure shows, the maximum of the probability density indeed moves uniformly to the right, as the black vertical bar indicates. We associate this movement with the group velocity that is simply given by $v_{\text{Group}}= p/m$ . One can define the phase velocity as a zero of the imaginary part, Im $\Psi(x)=0$ . The approximate positions of these zeros are indicated with the blue dashed vertical bars. For example, the thick blue dashed vertical bar indicates the zero that coincided with the vertical black bar at $t=0$ , at $x=0$ (see the first picture of this section). The phase velocities are clearly slower than the group velocity, but it seems that, after the wave packet passed, they even stall. This is indeed the case as the following graph shows:

Group and (approximate) phase velocities of the wave packet. These curves correspond to the black and blue vertical bars in the animation above.

Indeed, the first zero of the imaginary part (thick blue dashed line) initially moves with exactly half the group velocity,

$v_\text{phase}(t=0)=\frac{v_\text{group}}{2}=3$ ,

which is the relation derived in many textbooks by expanding the dispersion relation around the maximum of the momentum distribution. But, later, it slows down at later times, when the wave packet has already moved far to the right. The following four zeros (thin blue dashed lines) pick up velocity as the wave packet moves across them, and also become slower at later times once the packet passed over them.

This example shows that for a realistic wave packet, we indeed observe at some time that the phase velocity is exactly half the group velocity. But that statement holds only for a moment, and, in general, the phase velocity isn't constant over time, at all. In contrast, the group velocity, that we associate with the movement of a particle, does remain constant and obeys the classic relation $p=mv_\text{group}$ . Indeed, as the wave packet is symmetric (albeit getting wider over time), its expectation value just follows a classic trajectory according to Ehrenfest's theorem, $\langle x\rangle=v_\text{group}t$ .

But why does the wave packet get wider over time? This is a consequence of the uncertainty relation: At $t=0$ , the wave packet is confined to a certain spatial region with uncertainty $\Delta x$ given by the width of the Gaussian. The implies an uncertainty $\Delta p$ of the momenta in the wave packet according to $\Delta p\Delta x\geq\hbar/2$ . In fact, the Gaussian wave packet at $t=0$ is distinguished from other wave packets by being right at the uncertainty limit, $\Delta p\Delta x=\hbar/2$ . In other words, the smeared-out momentum distribution makes parts of the wave packet travel slower than $v_\text{group}$ and other parts travel faster. The net effect is a broadening of the wave packet over time, but, overall, it still moves with a constant $v_\text{group}$ .